25x2 + 56x + 21 + ( 10x + 11 )\(\sqrt{x+3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)
15 tháng 10 2023
b:
\(D=-25x^2+10x-1-10\)
\(=-\left(25x^2-10x+1\right)-10\)
\(=-\left(5x-1\right)^2-10< =-10\)
Dấu = xảy ra khi x=1/5
\(E=-9x^2-6x-1+20\)
\(=-\left(9x^2+6x+1\right)+20\)
\(=-\left(3x+1\right)^2+20< =20\)
Dấu = xảy ra khi x=-1/3
\(F=-x^2+2x-1+1\)
\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)
Dấu = xảy ra khi x=1
CM
27 tháng 2 2018
a) Ta có 3 x − 1 10 x 2 + 2 x . 25 x 2 + 10 x + 1 1 − 9 x 2 = − 5 x + 1 2 x ( 3 x + 1 )
b) Kết quả = p . ( p − 3 ) 7
NN
1
13 tháng 6 2019
đặt x+5=a\(\left(a\ge0\right)\) khi đó phương trình trở thành:
\(a^2-4+\sqrt{a}+\sqrt{16-a}=0\)
lại có \(\sqrt{a}+\sqrt{16-a}\ge\sqrt{a+16-a}=4\)
nên ta có:
\(a^2-4+\sqrt{a}+\sqrt{16-a}\ge a^2\)
Suy ra \(0\ge a^2\)
\(\Rightarrow a=0\)hay x+5=0
\(\Leftrightarrow x=-5\)
H
14 tháng 6 2023
`1,(4x^3+3x^3):x^3+(15x^2+6x):(-3x)=0`
`<=> 4 + 3 + (-5x) + (-2)=0`
`<=> -5x+5=0`
`<=>-5x=-5`
`<=>x=1`
`2,(25x^2-10x):5x +3(x-2)=4`
`<=> 5x - 2 + 3x-6=4`
`<=> 8x -8=4`
`<=> 8x=12`
`<=>x=12/8`
`<=>x=3/2`
`3,(3x+1)^2-(2x+1/2)^2=0`
`<=> [(3x+1)-(2x+1/2)][(3x+1)+(2x+1/2)]=0`
`<=>( 3x+1-2x-1/2)(3x+1+2x+1/2)=0`
`<=>( x+1/2) (5x+3/2)=0`
`@ TH1`
`x+1/2=0`
`<=>x=0-1/2`
`<=>x=-1/2`
` @TH2`
`5x+3/2=0`
`<=> 5x=-3/2`
`<=>x=-3/2 : 5`
`<=>x=-15/2`
`4, x^2+8x+16=0`
`<=>(x+4)^2=0`
`<=>x+4=0`
`<=>x=-4`
`5, 25-10x+x^2=0`
`<=> (5-x)^2=0`
`<=>5-x=0`
`<=>x=5`
HJ
1
18 tháng 9 2019
pt => \(x^2+10x+21=9\left(x+3\right)+4\left(x+7\right)+36-36\sqrt{x+3}-24\sqrt{x+7}\)
\(+12\sqrt{x^2+10x+21}\) ( bình phuownng hai vế)
=> \(x^2-3x-70=-36\sqrt{x+3}-24\sqrt{x+7}+12\left(3\sqrt{x+3}+2\sqrt{x+7}-6\right)\)
=> \(x^2-3x-70=-72\)
=> \(x^2-3x+2=0\)
=> \(\orbr{\begin{cases}x=2\\x=1\end{cases}}\)( thỏa mãn điều kiện).
Thay x=1 vào phương trình ban đầu ta có: \(4\sqrt{2}=6+4\sqrt{2}-6\)( đúng) .
Thay x=2 vào phương trình ban đầu ta có: \(3\sqrt{5}=3\sqrt{5}+6-6\)( đúng)
Vậy x=1 và x=2 là ngiệm của phương trình ban đầu
HJ
1
DL
11 tháng 10 2019
ĐKXĐ : x lớn hơn hoặc bằng -3
Đặt \(\sqrt{x+3}\)=a, \(\sqrt{x+7}\)=b ( a,lớn hợn hoặc bằng 0, b lớn hơn 0)
=> \(\sqrt{x^2+10x+21}\)=ab
PT<=> ab=3a+2b-6
<=> ab-3a-2b+6=0
<=> a(b-3)-2(b-3)=o
<=> (a-2)(b-3)=0
<=>\(\orbr{\begin{cases}a-2=0\\b-3=0\end{cases}}\)
<=>\(\orbr{\begin{cases}a=2\\b=3\end{cases}}\)
TH1: a=2=> \(\sqrt{x+3}\)=2 <=> x+3=4<=> x=1 (t/m)
TH2: b=3 => \(\sqrt{x+7}\)=3 <=> x+7=9<=> x=2 (t/m)
Vậy phương trình có nghiệm x= 1;2
2V
1
12 tháng 10 2021
\(x^2-25=\left(x-5\right)\left(x+5\right)\\ x^2+10x+25=\left(x+5\right)^2\\ x^2-6x+xy-6y=x\left(x-6\right)+y\left(x-6\right)=\left(x+y\right)\left(x-6\right)\\ x^2-2x-y^2+1=\left(x-1\right)^2-y^2=\left(x-y-1\right)\left(x+y-1\right)\)
L
2
VT
26 tháng 12 2017
ta có pt
<=>\(\sqrt{\left(x+3\right)\left(x+7\right)}=3\sqrt{x+3}+2\sqrt{x+7}=6\)
đặt \(\sqrt{x+3}=a;\sqrt{x+7}=b\)
nên pt <=>\(ab=3a+2b-6\Leftrightarrow ab-3a-2b+6=0\)
\(\Leftrightarrow a\left(b-3\right)-2\left(b-3\right)=0\Leftrightarrow\left(a-2\right)\left(b-3\right)=0\)
đến đây thì dễ rồi
26 tháng 12 2017
biêu thức dài dài trong căn pt thành nhân tử là \(\sqrt{\left(x+3\right)\left(x+7\right)}\)
xong rùi bn pt thành nhân tử sẽ có dạng \(\left(\sqrt{x+3}-2\right)\left(\sqrt{x+7}-3\right)=0\)
đến day bn làm tiếp nhé
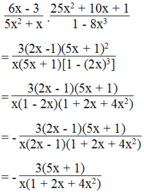
45 nha
$$$
@@@@@@@
HT