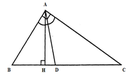
Cho ΔABC vuông tại A, AB=12cm, AC=16cm; đường phân giác góc A cắt BC tại D.
a) Tính BD,DC.
b) Vẽ đường cao AH, tính AH,HD,AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=9,6(cm)

Lời giải:
a) Vì tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}$
Mặt khác: $S_{ABC}=\frac{AH.BC}{2}$
$\Rightarrow AB.AC=AH.BC$ (đpcm)
b) Áp dụng định lý Pitago cho tam giác $ABC$ vuông:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
Áp dụng định lý Pitago cho tam giác $ABH$ vuông:
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+DC}=\frac{BD}{BC}=\frac{3}{3+4}$
$\Rightarrow BD=BC.\frac{3}{7}=\frac{60}{7}$ (cm)
$DC=BC-BD=20-\frac{60}{7}=\frac{80}{7}$ (cm)

a: Xét ΔHCA vuông tại H và ΔACB vuông tại A có
góc HCA chung
Do đó:ΔHCA\(\sim\)ΔACB
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\)
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
XétΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

A B C H
a ) Ta có : \(20^2=12^2+16^2\Leftrightarrow BC^2=AB^2+AC^2\)
Theo định lý Pytago đảo thì tam giác ABC là tam giác vuông
b )
Áp dụng hệ thức lượng vào tam giác vuông ABC ta có :
\(AB.AC=AH.BC\Leftrightarrow AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6\left(cm\right)\)
c ) Ta có :
\(AB.cosB+AC.cosC=\frac{AB.AB}{BC}+\frac{AC.AC}{BC}\)
\(=\frac{AC^2+AB^2}{BC}=\frac{BC^2}{BC}=BC=20\left(cm\right)\)
Chúc bạn học tốt !!!

a)\(\dfrac{SABD}{SACD}=\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{12}{16}=\dfrac{3}{4}\)
b) Vì \(\Delta ABC\) là tam giác vuông nên:
Áp dụng định lí Pi- ta- go: \(BC^2=AB^2+AC^2\\ BC^2=400\\ BC=20cm\)
c) Vì BC= BD + CD= 20 cm
và \(\dfrac{BD}{CD}=\dfrac{3}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\\ \left\{{}\begin{matrix}\dfrac{BD}{3}=\dfrac{20}{7}\Rightarrow BD=\dfrac{60}{7}cm\\\dfrac{CD}{4}=\dfrac{20}{7}\Rightarrow CD=\dfrac{80}{7}cm\end{matrix}\right.\)
d)\(SABC=\dfrac{1}{2}AH\cdot BC\\ \Rightarrow AH=\dfrac{SABC}{BC}=\dfrac{12\cdot16}{20}=\dfrac{48}{5}=9,6cm\)

a, Xét Δ AHC vuông tại H, có :
\(AB^2=AH^2+HB^2\)
=> \(AB^2=12^2+9^2\)
=> \(AB^2=225\)
=> AB = 15 (cm)
Xét Δ AHC vuông tại H, có :
\(AC^2=AH^2+HC^2\)
=> \(AC^2=12^2+16^2\)
=> \(AC^2=400\)
=> AC = 20 (cm)
Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go đảo)
=> Δ ABC vuông tại A

- Áp dụng định lý pitago vào tam giác ABC vuông tại A .
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
- Áp dụng hệ thức lượng vào tam giác ABC đường cao AH .
\(AH.BC=AB.AC\)
\(\Rightarrow AH=9,6\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ABH vuông tại H :
\(BH=\sqrt{AB^2-AH^2}=7,2\left(cm\right)\)
- Áp dụng định lý pitago vào tam giác ACH vuông tại H :
\(CH=\sqrt{AC^2-AH^2}=12,8\left(cm\right)\)
Ta có : AD là đường phân giác của tam giác ABC .
\(\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BD+CD}=\dfrac{AB+AC}{BC}=1,4\)
=> BD = 60/7 (cm )
=> HD = BD - BH = 48/35 (cm ) .

Xét tam giác vuông ABC ta có:

Vì AD là phân giác góc A nên theo tính chất đường phân giác trong tam giác ta có:
B D A B = D C A C ⇔ B D 12 = D C 16 = B D + D C 12 + 16 = B C 28 = 20 28 = 5 7
Suy ra BD = 12. 5 7 = 60 7 cm
Theo hệ thức lượng trong tam giác vuông ABC ta có:
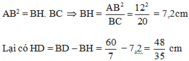
Đáp án cần chọn là: A

Hình bn tự vẽ nhan
a/Ta có : góc A+góc B+góc C=180độ =>gócB=
góc-AgócC=90độ-45độ=45độ
sinC=AB/BC=>BC=AB/sinC
<=>BC=10/sin45độ=10√2cm
Xét tam giác ABC,gócA=90độ có:
BC^2=AB^2+AC^2(pytago)
=>AC^2=BC^2-AB^2
AC^2=(10√2)^2-10^2=100
AC=√100=10cm
Lời giải:
a) Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=20$ (cm)
Theo tính chất đường phân giác:
$\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BC}=\frac{3}{7}\Rightarrow BD=BC.\frac{3}{7}=20.\frac{3}{7}=\frac{60}{7}$ (cm)
$CD=BC-BD=\frac{80}{7}$ (cm)
b)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD=BD-BH=\frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD=\sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
Hình vẽ: