Chứng minh rằng trong ngũ giác ,tổng các đường chéo lớn hơn chu vi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chứng minh rằng trong một ngũ giác, tổng các đường chéo lớn hơn chu vi.
Xét ngũ giác ABCDE cần chứng minh rằng:
AC+AD+BD+BE+CE>AB+BC+CD+DE+EAAC+AD+BD+BE+CE>AB+BC+CD+DE+EA
Gọi M, N lần lượt là giao điểm của BE và AD, AC.
P, Q lần lượt là giao điểm của BD với AC, CE.
K là giao điểm của CE và AD.
Quảng cáo
ΔNABΔNAB có AN+BN>ABAN+BN>AB (BĐT tam giác)
Tương tự ΔPBCΔPBC có BP+CP>BC,ΔQCDBP+CP>BC,ΔQCD có CQ+DQ>CDCQ+DQ>CD
ΔKDEΔKDE có DK+EK>DE,ΔMAEDK+EK>DE,ΔMAE có AM+EM>EAAM+EM>EA
Do đó AN+BN+BP+CP+CQ+DQ+DK+EK+AM+EM>AB+BC+CD+DE+EAAN+BN+BP+CP+CQ+DQ+DK+EK+AM+EM>AB+BC+CD+DE+EA
Mà
AC+AD+BD+BE+CE>(AN+CP)+(DK+AM)+(BP+DQ)+(EM+BN)+(CQ+EK)=AN+CP+DK+AM+BP+DQ+EM+BN+CQ+EK=AN+BN+BP+CP+CQ+DQ+DK+EK+AM+EMAC+AD+BD+BE+CE>(AN+CP)+(DK+AM)+(BP+DQ)+(EM+BN)+(CQ+EK)=AN+CP+DK+AM+BP+DQ+EM+BN+CQ+EK=AN+BN+BP+CP+CQ+DQ+DK+EK+AM+EM
Vậy AC+AD+BD+BE+CE>AB+BC+CD+DE+EAAC+AD+BD+BE+CE>AB+BC+CD+DE+EA

Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi tứ giác đó và nhỏ hơn chu vi tứ giác đó:
*Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm)
* giao của AC và BD là O.
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC
cổng 4 bất đẳng thức cùng chiề này lại ta có:
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm)

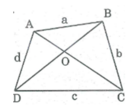
Đặt độ dài a = AB, b = BC, c = CD, d = AD
Gọi O là giao điểm 2 đường chéo AC và BD.
* Trong ∆ OAB, ta có:
OA + OB > a (bất đẳng thức tam giác) (1)
* Trong ∆ OCD, ta có:
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c hay AC + BD > a + c (*)
* Trong ∆ ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)
* Trong ∆ OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra:
OA + OB + OC + OD > b + d hay AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
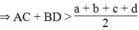
* Trong ∆ ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
* Trong ∆ ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
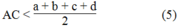
* Trong ∆ ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
* Trong ∆ BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
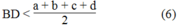
Từ (5) và (6) suy ra: AC + BD < a + b + c + d

Gọi O là giao của AC và BD
AB>AO+BO
AD>AO+DO
BC>BO+CO
DC>DO+CO
=>AB+AD+BC+CD>2(AC+BD)
=>(AC+BD)<P/2
AC<AB+BC
AC<AD+DC
BD<BC+CD
BD<AB+AD
=>2(AC+BD)<2*C ABCD
=>AC+BD<C ABCD

A B C D O
- Theo bất đẳng thức tam giác , ta có : \(AO+OB>AB\)
\(OB+OC>BC\)
\(OC+OD>CD\)
\(OD+OA>AD\)
\(\Rightarrow2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\Leftrightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\)
- Tương tự, ta có : \(AC< AB+BC\) ; \(AC< AD+CD\)
\(BD< AB+AD\) ; \(BD< BC+CD\)
\(\Rightarrow2\left(AC+BD\right)< 2\left(AB+BC+CD+AD\right)\Leftrightarrow AC+BD< AB+BC+CD+AD\)
Vậy ta có : \(\frac{AB+BC+CD+AD}{2}< AC+BD< AB+BC+CD+AD\)
Đặt độ dài AB = a, BC = b, CD = c, AD = d
Gọi O là giao điểm hai đường chéo AC và BD
Trong ∆OAB, ta có:
OA + OA > a (bất đẳng thức tam giác) (1)
Trong ∆OCD ta có:
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c
Hay AC + BD > a + c (*)
-Trong ∆OAD ta có: OA + OD > d (bất đẳng thức tam giác) (3)
-Trong ∆OBC ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: OA + OD + OB + OC > b + d
⇒ AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
⇒AC+BD>a+b+c+d2⇒AC+BD>a+b+c+d2
-Trong ∆ABC ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
-Trong ∆ADC ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
AC<a+b+c+d2AC<a+b+c+d2 (5)
-Trong ∆ABD ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
-Trong ∆BCD ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
BD<a+b+c+d2BD<a+b+c+d2 (6)
Từ (5) và (6) suy ra: AC + BD < a + b + c + d
Bạn ơi vẽ hình kiểu gì vậy