Cho tam giác ABC, M là trung điểm của cạnh BC. Trên tia đối của
tia MA lấy điểm D sao cho MD = MA
a) Chứng minh rằng: DMAC = DMDB
b) Chứng minh rằng: AC // BD
c) Trên các đoạn thẳng AC, BD lần lượt lấy các điểm E, F sao cho CE = BF. Chứng
minh rằng: M, E, F thẳng hàng
mong mn giúp câu c ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

a: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD
c: Xét tứ giác BFCE có
BF//CE
BF=CE
=>BFCE là hình bình hành
=>BC cắt FE tại trung điểm của mỗi đường
=>M,E,F thẳng hàng

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//CA
c: Xét ΔABC và ΔDCB có
AB=DC
BC chung
AC=DB
=>ΔABC=ΔDCB
d: Xét tứ giác AEDF có
AE//DF
AE=DF
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng

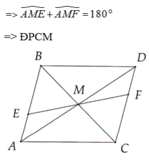
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AC//BD