Một người đứng ở độ cao 45 m so với mặt đất. Ném một hòn đã theo phương ngang. Bỏ qua sức cản của không khí. Lấy g = 10=m/s . Tính a) . Khoảng thời gian tử lúc ném đá cho đến khi nó chạm đất. b) Tầm bay xa của hòn đá.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 2 2018
Đáp án D
Góc tọa độ tại mặt đất, chiều dương theo phương thẳng đứng hướng xuống
Khi vật được ném từ mặt đất đến vị trí cao nhất cật chuyển động chậm dần đều:
Đến vị trí cao nhất v = 0; suy ra:
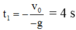
Sau đó vật rơi tự do chạm mặt đất với thời gian
Thời gian từ lúc ném đến khi vật chạm đất là:
VT
23 tháng 10 2019
Chọn D.
Chọn trục tọa độ thẳng đứng, gốc tọa độ tại vị trí ném, chiều dương hướng lên.
Phương trình chuyển động của vật: x = 40t – 0,5.10.t2 = 40t – 5t2
Khi vật chạm đất x = 0 → 40t – 5t2 = 0 → t = 8s.
LD
27 tháng 12 2023
* Tóm tắt : | Giải :
\(v_0=12\) m/s | a, Thời gian hòn đá chạm mặt biển :
\(h=19,6m\) | \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.19,6}{9,8}}=2\left(s\right)\)
\(g=9,8\) (m/s2) | b, Tầm Xa của hòn đá :
( đề ko cho, tức | \(L=v_o.t=12.2=24\left(m\right)\)
là g = 9,8)
----------
a, \(t=?\left(s\right)\)
b, \(L=?\left(m\right)\)\(\)
22 tháng 11 2023
a)Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0^2}x^2=\dfrac{9,8}{2\cdot5^2}x^2=0,196x^2\)
b)Thời gian hòn đá chạm mặt nước biển: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=2,04s\)
c)Tầm xa vật: \(L=x_{max}=v_0t\)
Tọa độ Ox: \(\left\{{}\begin{matrix}v_{0x}=v_0\\a_x=0\\v_x=v_0\end{matrix}\right.\)
Tọa độ Oy: \(\left\{{}\begin{matrix}v_{0y}=0\\a_y=g\\v_y=gt\end{matrix}\right.\)
Độ lớn vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}\)
c)Sau 1s:
Tầm xa: \(L=v_0t=5\cdot1=5m\)
Độ lớn: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(9,8\cdot1\right)^2+5^2}=11m/s\)
24 tháng 12 2022
a)Thời gian hòn đá rơi chạm mặt nước biển:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{10}{7}s\approx1,43s\)
b)Tầm xa của vật: \(L=v_0\sqrt{\dfrac{2h}{g}}=5\cdot\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{50}{7}m\)
Vận tốc vật khi chạm mặt nước biển:
\(v=v_0+gt=5+9,8\cdot\dfrac{10}{7}=19m/s\)
= 14,14m/s.
HQ
17 tháng 2 2021
Ta có: \(y=\dfrac{1}{2}gt^2\)
Khi chạm đất \(y=h=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2h}{g}}\) (1)
\(v=\sqrt{v_x^2+v_y^2}=\sqrt{v_0^2+\left(gt\right)^2}\) (2)
Từ (1) và (2) ta có công thức vận tốc v của vật khi chạm đất là: \(v=\sqrt{v_0^2+2gh}=10\sqrt{2}\simeq14,14\left(m/s\right)\)
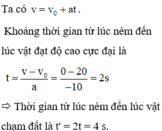
\(t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot45}{10}}=3s\)
\(L=v_0\cdot t=3v_0\)