mọi người ơi 1+1= mấy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo mệnh giá trên diễn đàn, \(1coin\) có giá tương ứng \(=10xu\) hoặc \(1\) nghìn đồng.

Em trả lời nhiều lắm cũng có nhiều người cho em đúng mà sao em ko lên đc



Với n = 0 thì \(\sqrt{1^3+2^3+3^3+..+n^3}=1+2+3+...+n\)(1)
Với n = 1 thì (1) đúng
Giả sử với n = k thì (1) đúng
Ta chứng minh với n = k + 1 thì (1) đúng
Tức là chứng minh khi \(\sqrt{1^3+2^3+3^3+...+k^3}=1+2+3+...+k\)
thì \(\sqrt{1^3+2^3+...+\left(k+1\right)^3}=1+2+3+...+k+1\)(2)
Từ (2) \(\Rightarrow1^3+2^3+3^3+...+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2\)
Khi đó (1 + 2 + 3 + ... + k + 1)2 = [(k + 1)(k + 2) : 2]2 = \(\frac{\left[\left(k+1\right)\left(k+2\right)\right]^2}{4}\)(3)
Lại có \(1^3+2^3+3^3+...+k^3+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2+\left(k+1\right)^3\)
\(=\frac{k^2\left(k+1\right)^2}{4}+\left(k+1\right)^3=\left(k+1\right)^2\left[\frac{k^2}{4}+k+1\right]\)
\(=\frac{\left(k+1\right)^2\left(k^2+4k+4\right)}{4}=\frac{\left(k+1\right)^2\left(k+2\right)^2}{4}=\frac{\left[\left(k+1\right)\left(k+2\right)\right]^2}{4}\)(4)
Từ (3) (4) \(\Rightarrow1^3+2^3+3^3+...+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2\)
\(\Rightarrow\left(2\right)\text{đúng}\Rightarrow\text{đpcm}\)
đầu tiên ta có :
\(1+2+3+..+n=\frac{n\left(n+1\right)}{2}\) ( cái này thì dễ rồi ha)
ta sẽ chứng minh : \(1^3+2^3+..+n^3=\left[\frac{n\left(n+1\right)}{2}\right]^2\) bằng quy nạp
đẳng thức đúng với n =1
giả sử đẳng thức đúng với n=k , tức là :
\(1^3+2^3+..+k^3=\left[\frac{k\left(k+1\right)}{2}\right]^2\)
ta sẽ chứng minh đúng với n=k+1, thật vậy
ta có : \(1^3+2^3+..+k^3+\left(k+1\right)^3=\left[\frac{k\left(k+1\right)}{2}\right]^2+\left(k+1\right)^3=\left(k+1\right)^2\left[\frac{k^2}{4}+k+1\right]=\frac{\left(k+1\right)^2\left(k+2\right)^2}{4}\)
Vậy đẳng thức đúng với k+1, theo nguyên lý quy nạp ta có điều phải chứng minh

2. She asked me to help her.
1. Miss Hoa told Nga to try her best to improve her Math.
4. My father told us not to make so much noisy here.
3. She told the children to be quiet.
1. It's been a year since I last heard from him.
4. We solve this problem by ourselves.
\(_{\text{sai cho mk xl}}\)



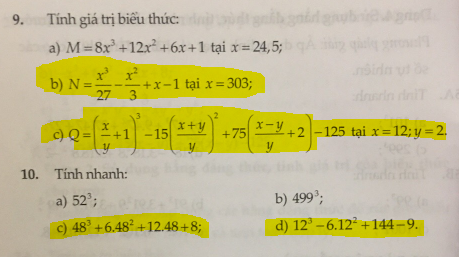 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 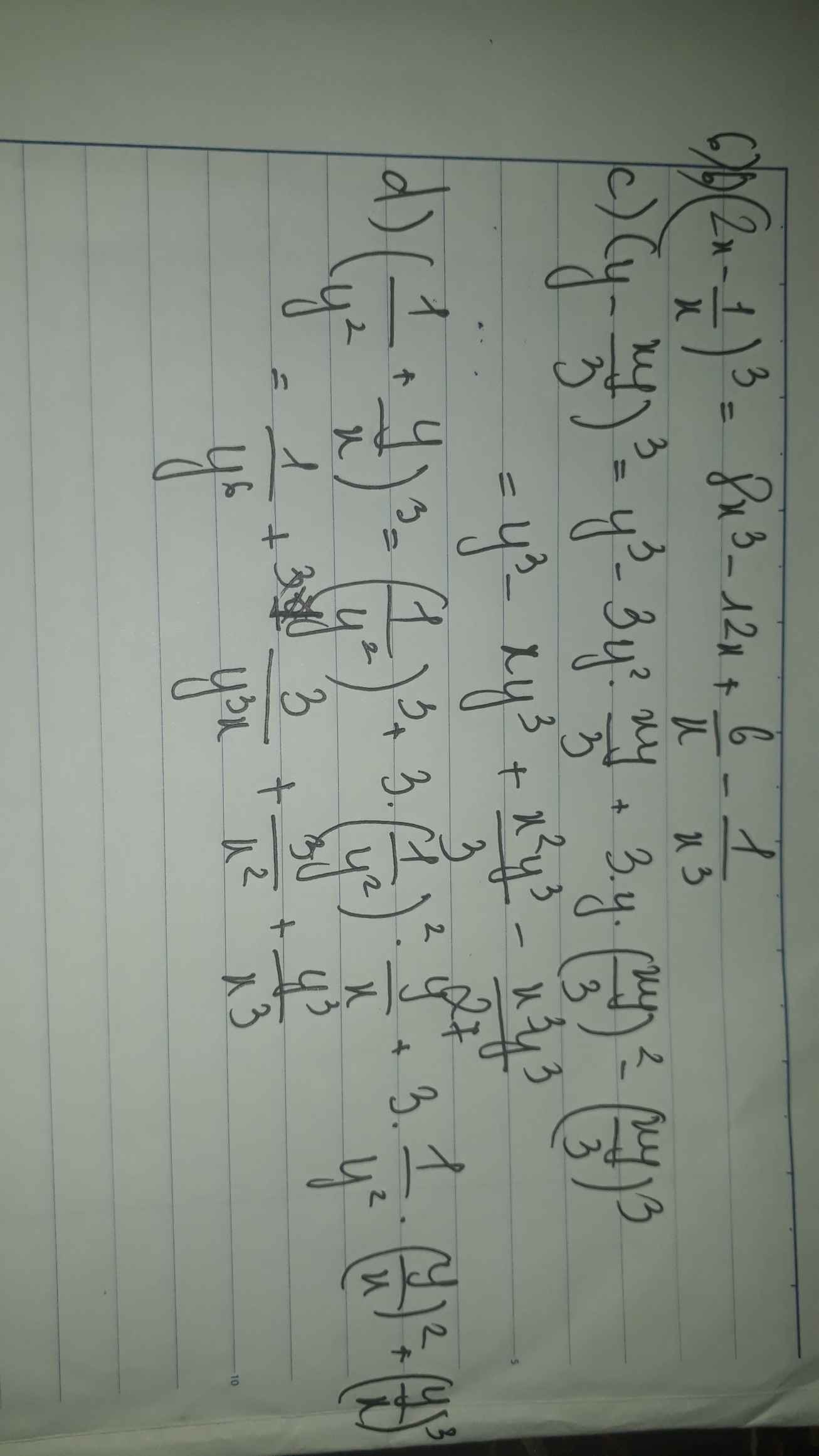
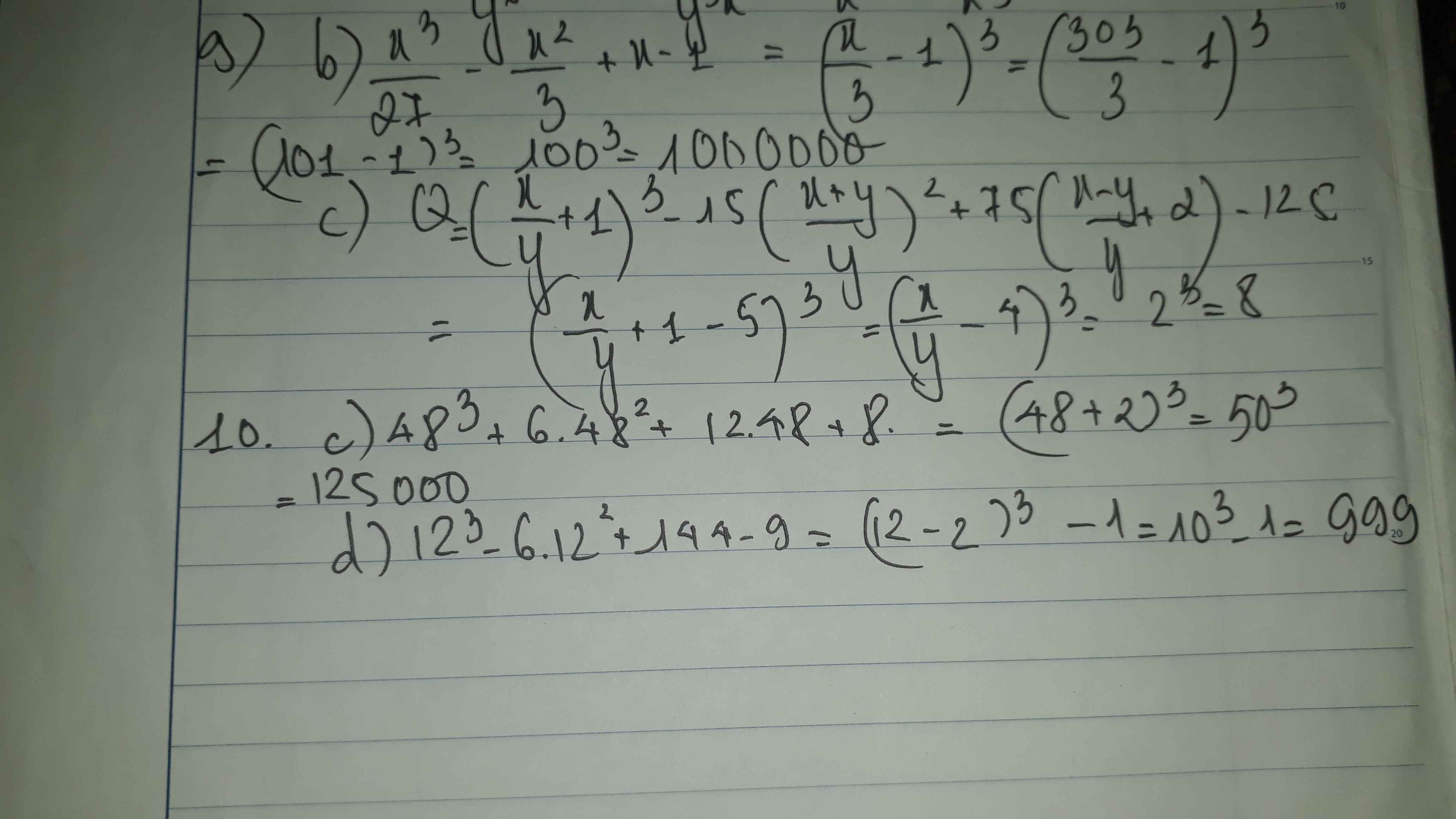



=2
nha bạn
HT
2 nhé chị