Cho ba tia OA;OB;OC tạo thành ba góc bằng nhau và không có điểm trong chung là AOB, BOC và COA. Vì sao có thể khẳng định tia đối của mỗi tia nói trên là tia phân giác của góc tạo bới hai tia còn lại ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DS
20 tháng 2 2018
tia coa nằm giữa hai tia còn lại
giải thích dựa vào số đo góc nha bn
CM
2 tháng 8 2017
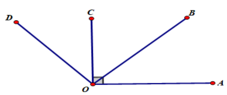
Trên nửa mặt phẳng bờ chứa tia OA, có A O B ^ = 45 ° , A O C ^ = 90 ° ⇒ A O B ^ < A O C ^ ( 45 ° < 90 ° ) nên OB nằm giữa hai tia OA và OC
CM
25 tháng 11 2018
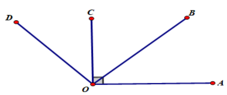
Trên nửa mặt phẳng bờ chứa tia OA có: A O C ^ = 90 o , A O D ^ = 120 o . ⇒ A O C ^ < A O D ^ nên OC nằm giữa OD và OA.
7 tháng 3 2020
+)Trên cùng một nửa mặt phẳng ta có:\(\widehat{AOB}< \widehat{AOC}\)(vì 62o<137o)
=>Tia OB nằm giữa 2 tia OA và OC
Chúc bn học tốt
PT
1
CM
23 tháng 5 2019
Vẽ hình:
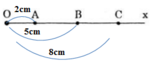
- Vì A, B nằm trên tia Ox mà OA (= 2cm) < OB (= 5cm) nên A nằm giữa O và B.
Ta có: OA + BA = OB suy ra BA = OB - OA = 5 - 2 = 3cm
- Vì B, C nằm trên tia Ox mà OB (= 5cm) < OC (= 8cm) nên B nằm giữa O và C.
Ta có: OB + BC = OC suy ra BC = OC - OB = 8 - 5 = 3cm
Ta thấy BA = 3cm; BC = 3cm nên BA = BC.
CM
20 tháng 1 2019
Đáp án là A
Vì A thuộc tia Ox, B thuộc tia Ax nên A nằm giữa O và B
⇒ OA + AB = OB ⇒ OB = 2 + 4 = 6cm
Trên tia BA có: BC < BA suy ra, C nằm giữa A và B
⇒ BC + AC = AB ⇒ AC = AB - BC = 4 - 3 = 1cm
Vì A nằm giữa O và C
⇒ OA + AC = OC ⇒ OC = 2 + 1 = 3cm
Vậy OB > OC
BT
0