Cho 4sin4x + 3cos4x = 7/4 .Tính A = 3sin4x + 4cos4x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2020
\(\text{c) }sin3x-\sqrt{3}cos3x=2cos5x\\ \Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=cos5x\\ \Leftrightarrow sin\frac{\pi}{6}\cdot sin3x-cos\frac{\pi}{6}\cdot cos3x=cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=-cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=cos\left(\pi-5x\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=\pi-5x+m2\pi\\3x+\frac{\pi}{6}=5x-\pi+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{48}+\frac{m\pi}{4}\\x=\frac{7\pi}{12}-n\pi\end{matrix}\right.\)
\(d\text{) }sinx\left(sinx+2cosx\right)=2\\ \Leftrightarrow cos^2x+\left(sinx-cosx\right)^2=0\\ \Leftrightarrow cosx=sinx=0\left(VN\right)\)
\(e\text{) }\sqrt{3}\left(sin2x+cos7x\right)=sin7x-cos2x\\ \Leftrightarrow\sqrt{3}sin2x+cos2x=sin7x-\sqrt{3}cos7x\\ \Leftrightarrow sin2x\cdot\frac{\sqrt{3}}{2}+cos2x\cdot\frac{1}{2}=sin7x\cdot\frac{1}{2}-cos7x\cdot\frac{\sqrt{3}}{2}\\ \Leftrightarrow sin2x\cdot cos\frac{\pi}{3}+cos2x\cdot sin\frac{\pi}{3}=sin7x\cdot cos\frac{\pi}{3}-cos7x\cdot sin\frac{\pi}{3}\\ \Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(7x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=7x-\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=\frac{4\pi}{3}-7x+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-m2\pi}{5}\\x=\frac{5\pi}{27}+\frac{n2\pi}{9}\end{matrix}\right.\)
15 tháng 7 2020
\(\text{a) }\sqrt{3}sin2x-cos2x+1=0\\ \Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=-\frac{1}{2}\\ \Leftrightarrow cos\frac{\pi}{3}\cdot cos2x-sin\frac{\pi}{3}\cdot sin2x=\frac{1}{2}\\ \Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos\frac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+m\pi\\x=n\pi\end{matrix}\right.\)
\(\text{b) }pt\Leftrightarrow sin4x=\frac{1-4cosx}{3}\\ \Leftrightarrow sin^24x+cos^24x=\left(\frac{1-cos4x}{3}\right)^2+cos^24x=1\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{arccos\left(-\frac{4}{5}\right)}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
CM
26 tháng 5 2018
Hướng dẫn giải
Chọn B.
Ta có: 4sin4 + 12cos2 x – 7 =0
ó 4sin4x – 12sin2 x + 5= 0
HP
31 tháng 7 2021
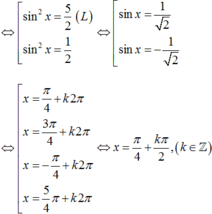
\(3cos4x+\left(cos2x-sinx\right)^2\)
\(=3cos4x+\left(\left|cos2x-sinx\right|\right)^2\)
\(\le3cos4x+\left[\left|cos2x\right|+\left|sin\left(-x\right)\right|\right]^2\)
\(\le3cos4x+2\left(cos^22x+sin^2x\right)\)
\(=8cos^22x+2sin^2x-3\)
\(=8cos^22x-cos2x-2\le7\)
Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}cos2x=-1\\cos2x.sin\left(-x\right)\ge0\\cos2x=sin\left(-x\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2021
\(6sinx.cos4x+4sin^2x-8sinx+3cos4x+2sinx-4+4cos^2x=3\)
\(\Leftrightarrow6sinx.cos4x-6sinx+3cos4x-3=0\)
\(\Leftrightarrow cos4x\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(cos4x-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
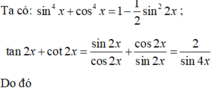
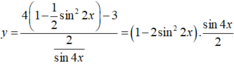
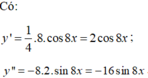
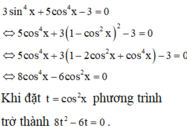
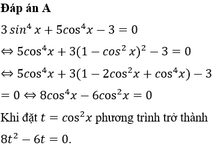
Ta có:
\(\left\{{}\begin{matrix}sin^2x+cos^2x=1\\4sin^4x+3cos^4x=\dfrac{7}{4}\end{matrix}\right.\)
\(\Rightarrow4sin^4x+3\left(1-sin^2x\right)^2=\dfrac{7}{4}\)
\(\Leftrightarrow7sin^4x-6sin^2x+\dfrac{5}{4}=0\) \(\Rightarrow\left[{}\begin{matrix}sin^2x=\dfrac{1}{2}\Rightarrow cos^2x=\dfrac{1}{2}\\sin^2x=\dfrac{5}{14}\Rightarrow cos^2x=\dfrac{9}{14}\end{matrix}\right.\)
Do đó: \(\left[{}\begin{matrix}A=\dfrac{7}{4}\\A=\dfrac{57}{28}\end{matrix}\right.\)