Đề bài: Giải phương trình dưới đây.
Mọi người giải giúp mình với ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Rightarrow\dfrac{1}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{1}{\left(2x-2\right)\left(2x-3\right)}+\dfrac{1}{\left(2x-3\right)\left(2x-4\right)}+\dfrac{1}{\left(2x-4\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-2}-\dfrac{1}{2x-1}+\dfrac{1}{2x-3}-\dfrac{1}{2x-2}+\dfrac{1}{2x-4}-\dfrac{1}{2x-3}+\dfrac{1}{2x-5}-\dfrac{1}{2x-4}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-5}-\dfrac{1}{2x-1}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{4}{\left(2x-1\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\left(2x-1\right)\left(2x-5\right)=21\)
\(\Rightarrow4x^2-12x-16=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)

\(\dfrac{x+2}{x-1}=\dfrac{x-1}{x-3}\) (1)
ĐKXĐ: \(x\ne1;x\ne3\)
(1) \(\Leftrightarrow\left(x+2\right)\left(x-3\right)=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-3x+2x-6=x^2-2x+1\)
\(\Leftrightarrow-3x+2x+2x=1+6\)
\(\Leftrightarrow x=7\) (nhận)
Vậy S = {7}

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

1. have waited
2. has written
3. has studied
4. has finished
5 haven't done
6. We don't go to school on Saturdays
7. They usually hold a party on New Year's Eve
8. I have seen this film already
9. Last night she came home between 10.30 and 11 o'clock
10. We are going to see the movie Dream City at 7.00 this evening
1 have waited
2 has written
3 has studied
4 has finished
5 haven't done
6 We don't go to school on Saturdays.
7 They usually hold a party in New Year's Eve.
8 I've seen this film already.
9 Last night, she came home between 10.30 and 11 o'clock.
10 We are going to see the movie Dream City at 7.00 this evening.

\(x^2\left(x+4,5\right)=13,5\)
<=>\(x^3+4,5x^2-13,5=0\)
<=> \(x^3+3x^2+1,5x^2+4,5x-4,5x-13,5=0\)
<=>\(x^2\left(x+3\right)+1,5x\left(x+3\right)-4,5\left(x+3\right)=0\)
<=>\(\left(x+3\right)\left(x^2+1,5x-4,5\right)=0\)
<=>\(\left(x+3\right)\left[x^2+3x-1,5-4,5\right]=0\)
<=>\(\left(x+3\right)\left[x\left(x+3\right)-1,5\left(x+3\right)\right]=0\)
<=>\(\left(x+3\right)^2\left(x-1,5\right)=0\)
<=> \(\left[{}\begin{matrix}\left(x+3\right)^2=0\\x-1,5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1,5\end{matrix}\right.\)
Vậy...
Ta có: \(x^2\left(x+4.5\right)=13.5\)
\(\Leftrightarrow x^3+\dfrac{9}{2}x^2-\dfrac{27}{2}=0\)
\(\Leftrightarrow2x^3+9x^2-27=0\)
\(\Leftrightarrow2x^3-3x^2+12x^2-18x+18x-27=0\)
\(\Leftrightarrow x^2\left(2x-3\right)+12x\left(2x-3\right)+9\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x^2+12x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x^2+12x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\\left(x+6\right)^2=27\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x+6=3\sqrt{3}\\x+6=-3\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\sqrt{3}-6\\x=-3\sqrt{3}-6\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};3\sqrt{3}-6;-3\sqrt{3}-6\right\}\)

x3 - 6xy + y3 = 8
<=> (x + y)3 - 3xy(x + y) - 6xy + 8 = 16
<=> (x + y + 2)(x2 + y2 - xy - 2x - 2y + 4) = 16
<=> \(\left(x+y+2\right)\left[\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\right]=16\)
Nhận thấy \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\ge0\)
=> x + y + 2 > 0
Khi đó 16 = 1.16 = 2.8 = 4.4
Lập bảng
| x + y + 2 | 1 | 16 | 4 | 2 | 8 | |
| \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\) | 16 | 1 | 4 | 8 | 2 | |
| x | ||||||
| y | | |
Đến đó bạn thế x qua y rồi làm tiếp nha

Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)
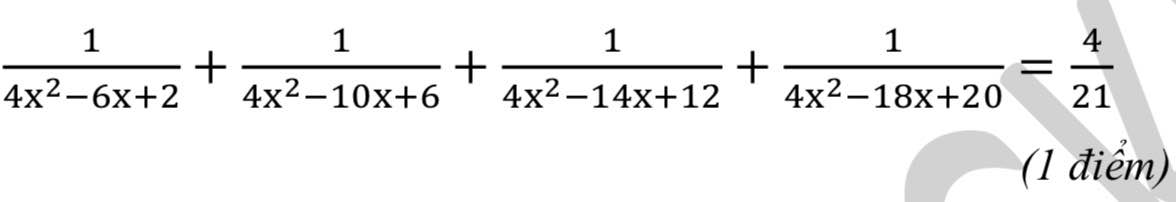



\(ĐK:x\ne\dfrac{1}{2};x\ne1;x\ne\dfrac{3}{2};x\ne2;x\ne\dfrac{5}{2}\\ PT\Leftrightarrow\dfrac{1}{\left(2x-1\right)\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(3x-2\right)}+\dfrac{1}{\left(3x-2\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(5x-2\right)}=\dfrac{4}{21}\\ \Leftrightarrow2\left[\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{1}{2}\right)\left(x-1\right)}+\dfrac{\dfrac{1}{2}}{\left(x-1\right)\left(x-\dfrac{3}{2}\right)}+\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{3}{2}\right)\left(x-2\right)}+\dfrac{\dfrac{1}{2}}{\left(x-2\right)\left(x-\dfrac{5}{2}\right)}\right]=\dfrac{4}{21}\)
\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{1}{2}}+\dfrac{1}{x-\dfrac{3}{2}}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-\dfrac{3}{2}}+\dfrac{1}{x-\dfrac{5}{2}}-\dfrac{1}{x-2}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{x-\dfrac{5}{2}-x+1}{\left(x-1\right)\left(x-\dfrac{5}{2}\right)}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{-\dfrac{3}{2}}{x^2-\dfrac{7}{2}x+\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow x^2-\dfrac{7}{2}x+\dfrac{5}{2}=-\dfrac{63}{4}\\ \Leftrightarrow4x^2-14x+10=-63\\ \Leftrightarrow4x^2-14x+73=0\\ \Leftrightarrow x\in\varnothing\)