NHIỆM VỤ 1: 1. Vẽ đồ thị hàm số y = 3x + 2 và y = 2x +3 trên cùng 1 hệ trục tọa độ 2. Gọi A là giao điểm của đường thẳng y = 3x + 2 với trục Ox; T là một điểm bất kỳ trên đường thẳng y 3x + 2 và T có tung độ dương. Xác định góc tạo bởi tia Ax và AT NHIỆM VỤ 2: 1. Vẽ đồ thị hàm số y= - 3x + 2 và y= - 2x +3 trên cùng 1 hệ trục tọa độ 2. Gọi A là giao điểm của đường thẳng y = -3x + 2 với trục Ox; T là một điểm bất kỳ trên đường thẳng y = -3x + 2 và T có tung độ dương. Xác định góc tạo bởi tia Ax và AT
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 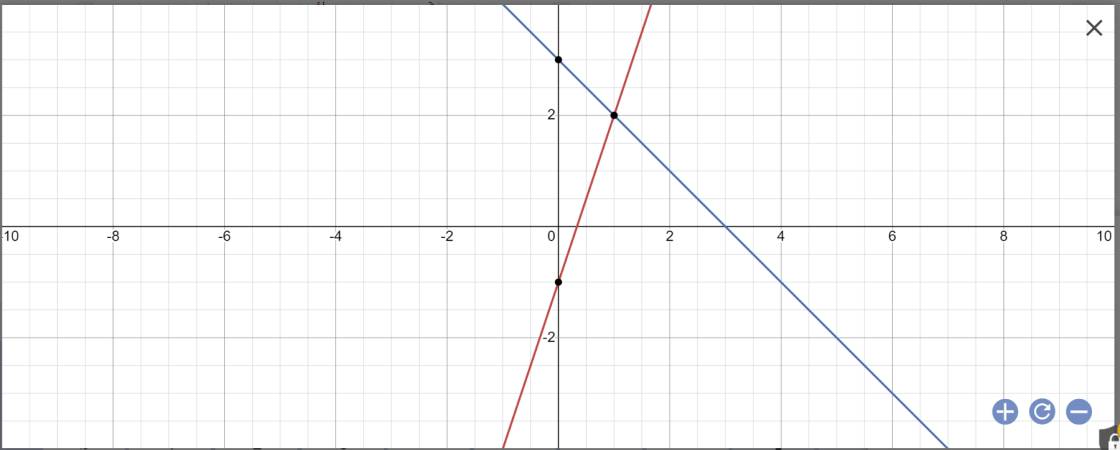
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)

a: Phương trình hoành độ giao điểm là:
3x-2=x-3
\(\Leftrightarrow2x=-1\)
hay \(x=-\dfrac{1}{2}\)
Thay \(x=-\dfrac{1}{2}\) vào y=x-3, ta được:
\(y=-\dfrac{1}{2}-3=\dfrac{-7}{2}\)

a:
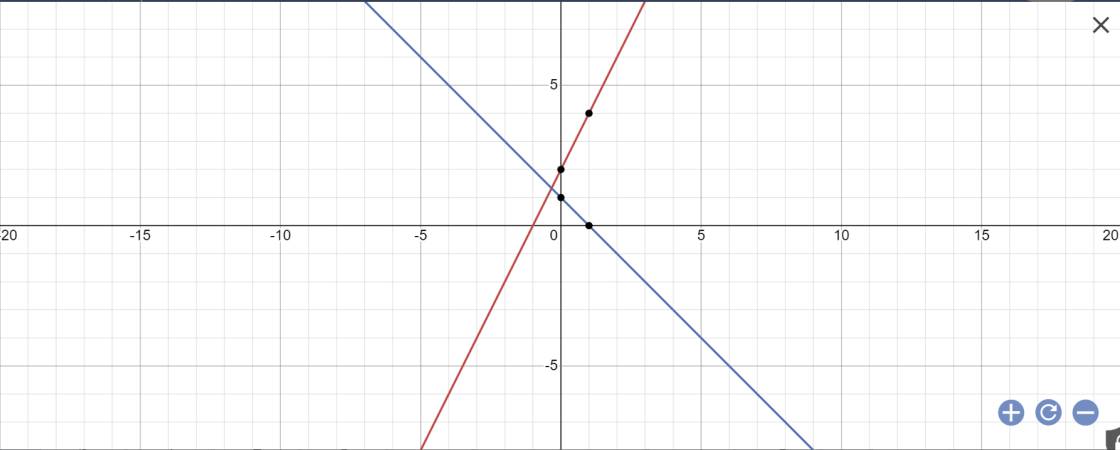
b: Phương trình hoành độ giao điểm là:
2x+2=-x+1
=>2x+x=1-2
=>3x=-1
=>\(x=-\dfrac{1}{3}\)
Khi x=-1/3 thì \(y=-\left(-\dfrac{1}{3}\right)+1=\dfrac{4}{3}\)
Vậy: \(M\left(-\dfrac{1}{3};\dfrac{4}{3}\right)\)
c: Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+1 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)

2: Vì y=2x+2//y=2x nên y=2x+2 và y=2x không có điểm chung
hay A không có tọa độ