Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có bộ gõ kí hiệu Toán mà :))
ĐK : a >= 0 ; a khác 36
\(K=\left[\frac{a+14\sqrt{a}+100}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}+\frac{\left(\sqrt{a}+6\right)\left(\sqrt{a}-6\right)}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}-\frac{\left(\sqrt{a}-7\right)\left(\sqrt{a}+7\right)}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\right]\div\left(\frac{\sqrt{a}-6}{\sqrt{a}-6}-\frac{\sqrt{a}-7}{\sqrt{a}-6}\right)\)
\(=\frac{a+14\sqrt{a}+100+a-36-a+49}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\div\frac{1}{\sqrt{a}-6}\)
\(=\frac{a+14\sqrt{a}+113}{\left(\sqrt{a}-6\right)\left(\sqrt{a}+7\right)}\cdot\left(\sqrt{a}-6\right)=\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}\)
Để K = 2 thì \(\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}=2\Rightarrow a+14\sqrt{a}+113=2\sqrt{a}+14\Leftrightarrow a+12\sqrt{a}+99=0\)
Với a >= 0 thì \(a+12\sqrt{a}+99\ge99>0\)=> Không có giá trị x thỏa mãn K = 2
Ta có : \(K=\frac{a+14\sqrt{a}+113}{\sqrt{a}+7}=\frac{\left(a+14\sqrt{a}+49\right)+64}{\sqrt{a}+7}=\frac{\left(\sqrt{a}+7\right)^2+64}{\sqrt{a}+7}\)
\(=\left(\sqrt{a}+7\right)+\frac{64}{\sqrt{a}+7}\ge2\sqrt{\left(\sqrt{a}+7\right)\cdot\frac{64}{\sqrt{a}+7}}=16\)( bđt AM-GM )
Dấu "=" xảy ra <=> \(\sqrt{a}+7=\frac{64}{\sqrt{a}+7}\Rightarrow a=1\left(tm\right)\). Vậy MinK = 16

a) \(\dfrac{5}{y}=\dfrac{1}{2}\)
\(y=\dfrac{5\times2}{1}=10\)
b) \(\dfrac{42}{25}:\dfrac{y}{5}=\dfrac{6}{5}\)
\(\dfrac{y}{5}=\dfrac{42}{25}:\dfrac{6}{5}\)
\(\dfrac{y}{5}=\dfrac{7}{5}\)
\(y=7\)

\(ƯCLN\left(a;b\right)=6\Rightarrow a=6a_1,b=6b_1\) (a1 và b1 nguyên tố cùng nhau)
Ta có: \(a+b=42\Rightarrow6\left(a_1+b_1\right)=42\Rightarrow a_1+b_1=7\)
Giả sử a < b thì a1 < b1 . Mà a1, b1 nguyên tố cùng nhau.
\(\Rightarrow a_1\in\left\{1;2;3\right\}\Rightarrow a\in\left\{6;12;18\right\}\Rightarrow b\in\left\{36;30;24\right\}\)
Vậy \(\left(a,b\right)\in\left\{\left(6;36\right),\left(12;30\right),\left(18;24\right)\right\}\) và các hoán vị của chúng.
a + b = 42, ƯCLN (a, b ) = 6
=> a = 6 . m ; b = 6 . n
Với ( m,n ) = 1
Mà : a + b = 42
Nên : 6 . m + 6 . n = 42
=> 6 . ( m + n ) = 42
=> ( m, n ) = 42 : 6
=> ( m, n ) = 7
| m | 1 | 2 | 3 | 4 | 5 | 6 |
| n | 6 | 5 | 4 | 3 | 2 | 1 |
Mà ( m,n ) = 1
=> ( m, n ) \(\in\){ ( 1,6 ) ; ( 2, 5 ) ; ( 3, 4 ) ; ( 4, 3 ) ; ( 5, 2 ) ; ( 6, 1 ) }
| m | 1 | 2 | 3 | 4 | 5 | 6 |
| a = 6. m | 6 | 12 | 18 | 24 | 30 | 36 |
| n | 6 | 5 | 4 | 3 | 2 | 1 |
| b = 6 . n | 36 | 30 | 24 | 18 | 12 | 6 |
Vậy \(\left(x,y\right)\in\left\{\left(6,36\right),\left(12,30\right),\left(18,24\right),\left(24,18\right),\left(30,12\right),\left(36,6\right)\right\}\)
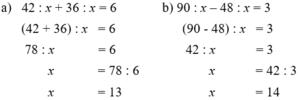
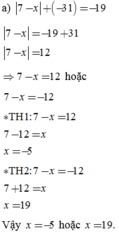

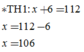
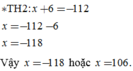
a : 6-6=42
a : 6 = 42 + 6
a : 6 = 48
a = 48 x 6
a = 288
Học tốt nha :333
Bằng 0