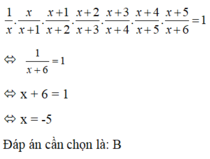A = 1/2 x (1+1/1x 3) x ( 1 +1/2x 4) x ( 1 + 1/3x 5) .... (1+1/2019x 2021)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
3 tháng 8 2020
Bài 1:
a) \(4x\left(3x-1\right)-2\left(3x+1\right)-\left(x+3\right)\)
\(=12x^2-4x-6x-2-x-3\)
\(=12x^2-11x-5\)
b) \(=\left(-2x^2-1xy+2y^2\right)\left(-1x^2y\right)\)
\(=\left[\left(-1x^2y\right)\left(-2x^2\right)\right]-\left[\left(-1x^2y\right).1xy\right]+\left[\left(-1x^2y\right).2y^2\right]\)
\(=\left(2x^4y\right)-\left(-1x^3y^2\right)+\left(-2x^2y^3\right)\)
\(=2x^4y+1x^3y^2-2x^2y^3\)
c) \(4x\left(3x^2-x\right)-\left(2x+3\right)^2\left(6x^2-3x+1\right)\)
\(=\left(4x.3x^2\right)-\left(4x.x\right)-\left[\left(2x\right)^2+2.2x.3+3^2\right]\left(6x^2-3x+1\right)\)
\(=12x^3-4x^2-\left(4x^2+12x+9\right)\left(6x^2-3x+1\right)\)
\(=12x^3-4x^2-\left[4x^2\left(6x^2-3x+1\right)+12x\left(6x^2-3x+1\right)+9\left(6x^2-3x+1\right)\right]\)
\(=12x^3-4x^2-\left[\left(24x^4-12x^3+4x^2\right)+\left(72x^3-36x^2+12x\right)+\left(36x^2-27x+9\right)\right]\)
\(=12x^3-4x^2-24x^4+12x^3-4x^2-72x^3+36x^2-12x-36x^2+27x-9\)
\(=-48x^3-8x^2-24x^4+15x-9\)
7 tháng 9 2021
a: \(A=\left(2x-5\right)^2-4x\left(x-5\right)\)
\(=4x^2-20x+25-4x^2+20x\)
=25
b: \(B=\left(4-3x\right)\left(4+3x\right)+\left(3x+1\right)^2\)
\(=16-9x^2+9x^2+6x+1\)
=6x+17
c: \(C=\left(x+1\right)^3-x\left(x^2+3x+3\right)\)
\(=x^3+3x^2+3x+1-x^3-3x^2-3x\)
=1
d: \(D=\left(2021x-2020\right)^2-2\left(2021x-2020\right)\left(2020x-2021\right)+\left(2020x-2021\right)^2\)
\(=\left(2021x-2020-2020x+2021\right)^2\)
\(=\left(x+1\right)^2\)
\(=x^2+2x+1\)
MC
11 tháng 7 2021
\(\left(x^2+3\right)\left(3-x^2\right)\)
\(\left(x^2+3\right)\left(-x^2+3\right)\)
\(\left(-x^2+3\right).x^2+3\left(-x^2+3\right)\)
\(-x^2.x^2+3x^2+3\left(-x^2+3\right)\)
\(-x^2.x^2+3x^2-3x^2+9\)
\(-x^2.x^2+9\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
13 tháng 12 2023
\(a,121-\left(115+x\right)=3x-\left(25-9-5x\right)-8\\ 121-115-x=3x-25+9+5x-8\\ 6-x=8x-24\\ 8x+x=-24-6\\ 9x=-30\\ x=-\dfrac{30}{9}=-\dfrac{10}{3}\\ ----\\ b,2^{x+2}.3^{x+1}.5^x=10800\\ \left(2.3.5\right)^x.2^2.3=10800\\ 30^x.12=10800\\ 30^x=\dfrac{10800}{12}=900=30^2\\ Vậy:x=2\)
CM
13 tháng 3 2019
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
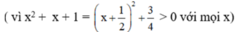
Quy đồng mẫu thức hai vế:
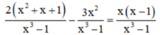
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
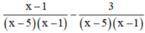
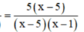
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
25 tháng 7 2015
rút gọn các đa thức bằng cách nhân chúng với nhau rồi thay số vào là tính được mà
3 tháng 10 2020
a) A = (x - 3)(x + 7) - (2x - 5)(x - 1)
= x(x + 7) - 3(x + 7) - 2x(x - 1) + 5(x - 1)
= x2 + 7x - 3x - 21 - 2x2 + 2x + 5x - 5
= (x2 - 2x2) + (7x - 3x + 2x + 5x) + (-21 - 5) = -x2 + 11x - 26 = -(x2 - 11x + 26)
+) Với x = 0 thì -(02 - 11.0 + 26) = -(0 - 0 + 26) = -26
+) Với x = 1 thì -(12 - 11.1 + 26) = -(1 - 11 + 26) = -16
b) B = (3x + 5)(2x - 1) + (4x - 1)(3x + 2)
= 3x(2x - 1) + 5(2x - 1) + 4x(3x + 2) - 1(3x + 2)
= 6x2 - 3x + 10x - 5 + 12x2 + 8x - 3x - 2
= (6x2 + 12x2) + (-3x + 10x + 8x - 3x)+ (-5 - 2) = 18x2 + 12x - 7
|x| = 2 => x = 2 hoặc x = -2
Với x = 2 thì 18.22 + 12.2 - 7 = 18.4 + 24 - 7 = 72 + 24 - 7 = 89
Với x = -2 thì 18.(-2)2 + 12.(-2) - 7 = 18.4 + (-24) - 7 = 18.4 - 24 - 7 = 41
c) C = (2x + y)(2z + y) + (x - y)(y - z)
= 2x(2z + y) + y(2z + y) + x(y - z) - y(y- z)
= 4xz + 2xy + 2zy + y2 + xy - xz - y2 + yz
= 4xz + 2xy + 2zy + (y2 - y2) +xy - xz + yz
= 4xz + 3xy + 3zy
Với x = 1,y = 1,z = 1
= 4.1.1 + 3.1.1 + 3.1.1 = 4 + 3 + 3 = 10