Một xe đang chuyển động với vận tốc 72km/h thì hãm phanh và chuyển động chậm dần đều. Xe còn đi được 40m thì dừng hẳn. Tìm gia tốc của xe, suy ra hệ số ma sát giữa xe và mặt đường?
Giúp em với ạ em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
10 tháng 1 2022
a) 72 km/h = 20 m/s
\(v_2^2\) - \(v_1^2\) = 2as
↔ 0 - \(20^2\) = 2.a.500
↔ -400 = 1000.a ↔ a = 0,4
➙ Gia tốc của xe là 0,4 \(m^2\)/s
b)
\(v_2\) - \(v_1\) = at
↔ 0 - 20 = -0,4t
↔ -20 = -0,4t ↔ t = \(\dfrac{-20}{-0,4}\) = 50 (giây)
10 tháng 1 2022
Nhấn vào \(\Sigma\) là gõ được cái \(\Leftrightarrow\) chứ đâu cần cái ↔️ nhỉ:)?
10 tháng 10 2021
Vật chuyển động chậm dần đều: \(a=-0,2\)m/s2
\(v_0=54\)km/h\(=15\)m/s
a) Vận tốc của xe sau 20s chuyển động:
\(v=v_0+at=15-0,2\cdot20=11\)m/s
b) Quãng đường xe đi từ lúc hãm phanh đến khi dừng hẳn(v'=0m/s) là:
\(v'^2-v^2_0=2aS\Rightarrow0-15^2=2\cdot\left(-0,2\right)\cdot S\)
\(\Rightarrow S=562,5m\)
VT
9 tháng 1 2017
Đáp án C.
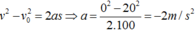
( Dấu - chứng tỏ a → ngược chiều với v → là chiều chuyển động và cũng là chiều dương của ).
- Vận tốc là một đại lượng véctơ nên giá trị của nó(trong một hệ tọa độ) có thể dương, âm hoặc bằng 0. Giá trị dương cho biết vật chuyển động theo chiều dương và ngược lại, giá trị âm cho biết vật chuyển động theo chiều âm của trục tọa độ.
- Tốc độ là đại lượng không âm, tốc độ tức thời là độ lớn của vận tốc tức thời
21 tháng 11 2021
\(v_0=72\)km/h=20m/s
Gia tốc xe: \(v^2-v^2_0=2aS\)
\(\Rightarrow a=\dfrac{v^2-v^2_0}{2S}=\dfrac{0-20^2}{2\cdot40}=-5\)m/s2
Ta có: \(-F_{hãm}-F_{ms}=m\cdot a\)
\(F_{hãm}=-F_{ms}-m\cdot a=-\mu mg-m\cdot a=-0,2\cdot1000\cdot10-1000\cdot\left(-5\right)=3000N\)
\(v_0=72\)km/h=20m/s
Gia tốc: \(v^2-v^2_0=2aS\)
\(\Rightarrow a=\dfrac{v^2-v^2_0}{2S}=\dfrac{0-20^2}{2\cdot40}=-5\)m/s2
Hệ số ma sát:
\(a=-\mu\cdot g\Rightarrow\mu=-\dfrac{a}{g}=-\dfrac{-5}{10}=0,5\)