giúp mình làm câu 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2021
Bài 11:
a: Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}-1\right)\)
\(=x-\sqrt{x}\)
b: Để P=2 thì \(x-\sqrt{x}-2=0\)
hay x=4
24 tháng 8 2021
Bài 10:
a: Ta có: \(A=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}\cdot\dfrac{x+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để A<0 thì \(\sqrt{x}-1< 0\)
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
Để A=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}+1\)
\(\Leftrightarrow x=0\)
c: Thay x=4 vào A, ta được:
\(A=\dfrac{4+2+1}{2-1}=7\)
14 tháng 8 2021
Bài 10: A
Bài 11:
Áp dụng hệ thức về cạnh và góc trong tam giác vào tam giác vuông, ta được:
AC = AB.tan\(^{50^0}\) = 21.tan\(^{50^0}\) \(\approx\) 25
BC = \(\dfrac{AB}{\sin C}\)= \(\dfrac{21}{sin40^0}\)\(\approx\)33
BD = \(\dfrac{AB}{\cos25^0}\)=\(\dfrac{21}{\cos25^0}\)\(\approx\)23
A
1
13 tháng 10 2021
Bài 10:
a: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-8=-2x-3\\y=3x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-8=-5\end{matrix}\right.\)
Thay x=1 và y=-5 vào (d3), ta được:
\(3m+2m+1=-5\)
hay \(m=-\dfrac{6}{5}\)
16 tháng 4 2022
Câu 11.
a)Độ tự cảm của ống dây:
\(L=4\pi\cdot10^{-7}\cdot\dfrac{N^2}{l}S=4\pi\cdot10^{-7}\cdot\dfrac{1000^2}{0,2}\cdot50\cdot10^{-4}=0,0314H=0,0314\cdot10^3=31,4mH\)
b)Độ biến thiên từ thông:
\(\Delta\Phi=L\cdot\Delta i=0,0314\cdot\left(1-0\right)=0,0314Wb\)
Suất điện động cảm ứng:
\(e_{tc}=\left|-\dfrac{\Delta\Phi}{\Delta t}\right|=\left|-\dfrac{0,0314}{0,1}\right|=0,314V\)
31 tháng 8 2021
1: Xét ΔAOC và ΔBOD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔAOC=ΔBOD
Suy ra: \(\widehat{ACO}=\widehat{BDO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
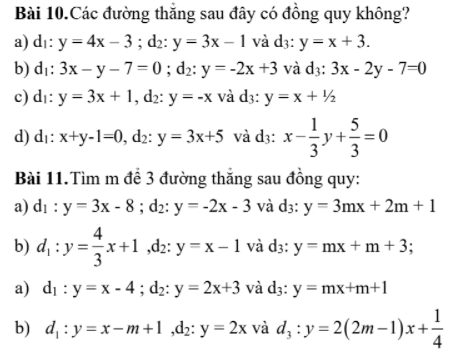
mờ quá
Không đọc được luôn