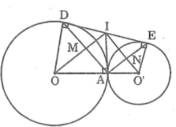
a) AE và DE là hai tiếp tuyến nên AE┴AO; DE┴DO => tứ giác EDOA nội tiếp đường tròn đường kính OE (1).
Hình Thang ABCD cân => AD=BC => hai cung tương ứng bằng nhau =>^BDC=^ACD = 1/2 số đo cung nhỏ AD.
^DIA=^IDC+^ICD (góc ngoài ∆DIC).
=>^DIA = 2 lần ^ICD = số đo cung nhỏ AD =^DOA => Tứ giác AOID nội tiếp (I và O cùng nhìn AD với góc bằng nhau) (2)
(1)&(2) => 5 điểm A,E,D,I,O cùng nằm trên đường tròn đường kính OE hay tứ giác AEDI nội tiếp.
b)
^BDC=^ACD (cmt) =>∆DIC cân =>đường trung trực của DC đi qua I. mà DC là một dây cung của (O) nên đường trung trực này cũng đi qua O => IO ┴ CD (3).
I nằm trên đường tròn đường kính OE (cmt) nên ^OIE=90° (góc nội tiếp chắn nửa đường tròn). =>EI ┴ OI (4).
(3)&(4)=> EI//DC hay EI//AB (vì AB//CD).
c)
Do RS//AB//DC nên áp dụng định lý Talét ta có CI/CA=DI/DB.
Trong ∆ADB ta có IR/AB=DI/DB.
Trong ∆ACB ta có IS/AB=CI/CA.
=>IR/AB=IS/AB => IR=IS hay I là trung điểm của RS.
d)
Xét ∆DAC ta có IR/DC=AI/CA
theo cmt ta có IR/AB=DI/DB=CI/CA
=>IR/DC+IR/AB=AI/CA+CI/CA=(AI+CI)/CA=1
=>IR/DC+IR/AB=1 Chia 2 vế chi IR ta có
=>1/DC+1/AB=1/IR
Mà RS=2.IR =>1/DC+1/AB=2/RS.
bạn nguyễn minh tâm ra nhận