mn giúp e
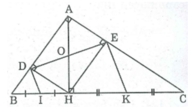
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.
a) CM: AH= DE
b) Gọi I là trung diểm HB, K là trung điểm HC. CMR: DI//EK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 12 2021
\(a,\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\\ \Rightarrow AEHD\text{ là hcn}\\ \Rightarrow AH=DE\\ b,DI\text{ là tt ứng cạnh huyền }BH\Rightarrow DI=IH\Rightarrow\widehat{IDH}=\widehat{IHD}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{EDH}=\widehat{AHD}\\ \Rightarrow\widehat{IDE}=\widehat{IDH}+\widehat{EDH}=\widehat{IHD}+\widehat{AHD}=\widehat{IHA}=90^0\\ \Rightarrow DI\perp DE\left(1\right)\\ EK\text{ là tt ứng cạnh huyền }CH\Rightarrow EK=KH\Rightarrow\widehat{KEH}=\widehat{KHE}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{AHE}=\widehat{DEH}\\ \Rightarrow\widehat{DEK}=\widehat{DEH}+\widehat{HEK}=\widehat{AHE}+\widehat{KHE}=\widehat{AHK}=90^0\\ \Rightarrow EK\perp DE\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI\text{//}EK\)
TB
18 tháng 11 2021
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
KV
22 tháng 10 2023
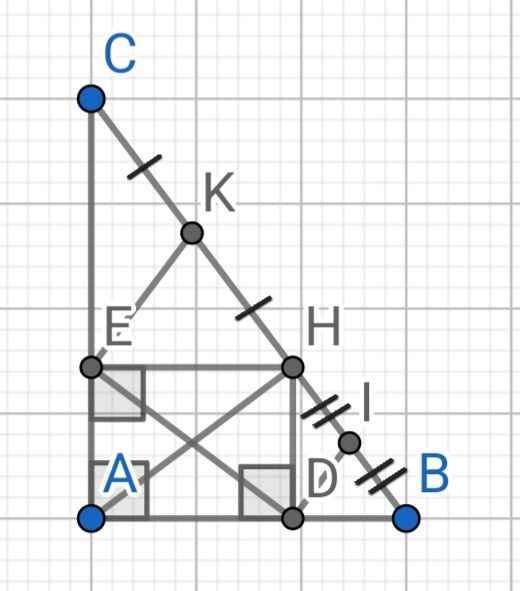a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE
CM
26 tháng 12 2017
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
TH
11 tháng 12 2021
cho tam giác ABC vuông tại A đường cao AH ( H thuộc cạnh BC) .gọi D, E theo thứ tự chân đường vuông góc kẻ từ H đến AB và AC .Gọi M, N theo thứ tự là trung điểm của BH và CH .Gọi I là giao điểm của AH và ED
1: cm tam giác DHE là tam giác vuông.Biết AB=3,AC=4, tính
a: bán kính của đường tròn ngoại tiếp tam giác DHE
b: cos ACH
2: cm ED là tiếp tuyến của đường tròn đg kính CH
3: cm I thuộc đg tròn đg kính Mn
23 tháng 9 2016
Viết thiếu đề: ... các đường vuông góc kẻ từ H đến AB, AC.
a) Cm. AH = DE
Ta có: HD vuông góc với BA (gt)
ED vuông góc với BA ( BA vuông góc với AC; E thuộc AC)
=> HD // EA
Ta lại có: DA vuông góc với AC ( BA vuông góc với AC; D thuộc AB)
HE vuông góc với AC (gt)
=> DA // HE
Xét tứ giác DHEA, có;
* HD // EA (cmt)
* DA // HE (cmt)
=> DHEA là hình bình hành (định nghĩa)
=> DE = AH (tính chất của đường chéo) (đpcm)
b) Gọi O là giao điểm của 2 đường chéo DE, AH của hình bình hành DHEA.
Xét tam giác HEC vuông tại E, có:
* K là trung điểm của HC (gt)
=> EK = KH = KC (trung tuyến của tam giác vuông bằng 1/2 cạnh huyền)
=> DI = IH = IB ( chứng minh tương tự)
Xét tam giác DIO và tam giác HIO, có:
* DI = IH (cmt)
* IO là cạnh chung
* OD = OH (DHEA là hình bình hành)
=> tam giác DIO = tam giác HIO (c.c.c)
=> góc IHO = góc IDO ( yếu tố tương ứng)
Mà góc IHO = 90 độ (AH là đường cao)
=> góc IDO = 90 độ
=> ID vuông góc với DE (1)
Xét tam giác HOK và tam giác EOK, có:
* HO = EO (DHEA là hình bình hành)
* OK là cạnh chung
* KH = KE (cmt)
=> tam giác HOK = tam giác EOK (c.c.c)
=> góc OHK = góc OEK ( yếu tố tương ứng)
Mà góc OHK = 90 độ (AH là đường cao)
=> góc OEK = 90 độ
=> KE vuông góc với DE (2)
Từ (1), (2) => ID // KE (từ vuông góc đến song song) (đpcm).
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
hay AH=DE
giúp e câu b luôn dc ko ạ