(x+4)chia hết (2x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 11 2021
2: \(\Leftrightarrow x+2\in\left\{1;-1\right\}\)
hay \(x\in\left\{-1;-3\right\}\)
HN
25 tháng 12 2018
Với tất cả các câu, mk chỉ làm ngắn gọn. Nếu bn muốn đầy đủ, thì bn tự lập bảng rồi xét.
1. \(13⋮\left(x-3\right)\)
\(\Leftrightarrow\left(x-3\right)\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
\(\Rightarrow x\in\left\{2;4;-10;16\right\}\)
Vậy x = ......................
2. \(\left(x+13\right)⋮\left(x-4\right)\)
\(\Leftrightarrow\left(x-4\right)+17⋮\left(x-4\right)\)
\(\Leftrightarrow17⋮x-4\)
\(\Leftrightarrow\left(x-4\right)\inƯ\left(17\right)=\left\{\pm1;\pm17\right\}\)
\(\Rightarrow x\in\left\{3;5;-13;21\right\}\)
Vậy x = ...................
3. \(\left(2x+108\right)⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)+105⋮\left(2x+3\right)\)
\(\Leftrightarrow105⋮\left(2x+3\right)\)
\(\Leftrightarrow\left(2x+3\right)\inƯ\left(105\right)\)\(=\left\{\pm1;\pm3;\pm5;\pm7;\pm15;\pm21;\pm35;\pm105\right\}\)
\(\Rightarrow x=-2;-1;-3;0;-4;1;-5;2;...............\)
4. \(17x⋮15\)
\(\Leftrightarrow x⋮15\) ( vì \(\left(15,17\right)=1\) )
Do đó : Với mọi x thuộc Z thì \(17x⋮15\)
HN
25 tháng 12 2018
6. \(\left(x+16\right)⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)+15⋮\left(x+1\right)\)
\(\Leftrightarrow15⋮\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\inƯ\left(15\right)=\left\{\pm1;\pm3;\pm5;\pm15\right\}\)
\(\Rightarrow x\in\left\{-2;0;-4;2;-6;4;-16;14\right\}\)
Vậy x = .....................
7. \(x⋮\left(2x-1\right)\)
Mà \(\left(2x-1\right)\) lẻ
Nên : Với mọi x thuộc Z là số lẻ thì \(x⋮\left(2x-1\right)\)
8. \(\left(2x+3\right)⋮\left(x+5\right)\)
\(\Leftrightarrow\left(2x+10\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow2.\left(x+5\right)-7⋮\left(x+5\right)\)
\(\Leftrightarrow7⋮\left(x+5\right)\)
\(\Leftrightarrow\left(x+5\right)\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-12;2\right\}\)
Vậy x = .........................
DH
3
28 tháng 11 2019
\(c,10⋮2x+1\)
\(\Rightarrow2x+1\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng
| 2x+1 | 1 | -1 | 2 | -2 | 5 | -5 | -10 | 10 |
| 2x | 0 | -2 | 1 | -3 | 4 | -6 | -11 | 9 |
| x | 0 | -1 | 1/2 | -3/2 | 2 | -3 | -11/2 | 9/2 |
\(d,x+13⋮x+1\)
\(x+1+12⋮x+1\)
\(\Rightarrow x+1⋮x+1\)
\(\Rightarrow12⋮x+1\)
\(\Rightarrow x+1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
Ta có bảng
| x+1 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 6 | -6 | 12 | -12 |
| x | 0 | -2 | 1 | -3 | 2 | -4 | 3 | -5 | 5 | -7 | 11 | -13 |
Bn tự KL cả 2 phần ...
28 tháng 11 2019
\(f,2x+108⋮2x+3\)
\(\Rightarrow\left(2x+3\right)+105⋮2x+3\)
\(\Rightarrow2x+3⋮2x+3\)
\(\Rightarrow105⋮2x+3\)
\(\Rightarrow2x+3\inƯ\left(105\right)=\left\{\pm1;\pm3;\pm7;\pm15;\pm21;\pm35;\pm105\right\}\)
Ta lập bảng xét
| 2x+3 | 1 | -1 | 3 | -3 | 7 | -7 | 15 | -15 | 21 | -21 | 35 | -35 | 105 | -105 |
| 2x | -2 | -4 | 0 | -6 | 4 | -10 | 12 | -18 | 18 | -24 | 32 | -38 | 102 | -108 |
| x | -1 | -2 | 0 | -3 | 2 | -5 | 6 | -9 | 9 | -12 | 16 | -19 | 51 | -54 |
Tự KL ....
8 tháng 4 2020
1) Ta có x+3=x+1+2
=> 2 chia hết cho x+1
=> x+1 \(\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
Ta có bảng
| x+1 | -2 | -1 | 1 | 2 |
| x | -3 | -2 | 0 | 1 |
2) Ta có 2x+5=2(x+2)+1
=> 1 chia hết cho x+2
=> x+2 =Ư (1)={-1;1}
Nếu x+2=-1 => x=-3
Nếu x+2=1 => x=-1
3, Ta có 3x+5=3(x-2)+11
=> 11 chia hết cho x-2
=> x-2 thuộc Ư (11)={-11;-1;1;11}
Ta có bảng
| x-2 | -11 | -1 | 1 | 11 |
| x | -9 | 1 | 3 | 13 |
8 tháng 4 2020
4) Ta có x2-x+2=(x-1)2-x
=> x chia hết cho x-1
Ta có x=x-1+1
=> 1 chia hết cho x+1
=> x+1 thuộc Ư (1)={-1;1}
Nếu x+1=-1 => x=-2
Nếu x+1=1 => x=0
5) Ta có x2+2x+4=(x+2)2-2x
=> 2x chia hết cho x+1
Ta có 2x=2(x+1)-2
=> x+1 thuộc Ư (2)={-2;-1;1;2}
Ta có bảng
| x+1 | -2 | -1 | 1 | 2 |
| x | -3 | -2 | 0 | 1 |
20 tháng 5 2022
a: Ta có \(x^3-4x^2+x-n⋮x-4\)
\(\Leftrightarrow x^2\left(x-4\right)+x-4+n+4⋮x-4\)
=>n+4=0
hay n=-4
b: ta có: \(4x^3-2x^2+2x+n⋮2x+1\)
\(\Leftrightarrow4x^3+2x^2-4x^2-2x+4x+2+n-2⋮2x+1\)
=>n-2=0
hay n=2
c: \(\Leftrightarrow x^4-3x^3+3x^3-9x^2+6x^2-18x+21x-63-n+63⋮x-3\)
=>63-n=0
hay n=63
10 tháng 12 2023
a: \(\left(-120\right):15+12\left(2x-1\right)=52\)
=>\(12\left(2x-1\right)-8=52\)
=>\(12\left(2x-1\right)=60\)
=>\(2x-1=\dfrac{60}{12}=5\)
=>2x=5+1=6
=>\(x=\dfrac{6}{2}=3\)
c: \(x+4⋮x+1\)
=>\(x+1+3⋮x+1\)
=>\(3⋮x+1\)
=>\(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
d: \(2x+7⋮x+2\)
=>\(2x+4+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
e: \(3x⋮x-1\)
=>\(3x-3+3⋮x-1\)
=>\(3⋮x-1\)
=>\(x-1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{2;0;4;-2\right\}\)
2 tháng 8 2015
a) 4 chia hết x-1
\(\Rightarrow x-1\in\left\{-1;-2;-4;1;2;4\right\}\)
\(x\in\left\{0;-1;-3;2;3;5\right\}\)
Các câu còn lại tương tương tự nha
mình chỉ giải bạn phần đầu các câu 2 ; 3 ; 5 ; 6 thôi
2) x+2 chia hết x+1
=> (x+2) - (x + 1) chia hết x+1
=> x+ 2 - x - 1 chia hết x + 1
=> 1 chia hết cho x +1 (trở lại giống bài 1 rồi chứ!!!!!!! tự làm tiếp nha ^^)
3) x+4 chia hết x
=> x+4 - x chia hết x
=> 4 chia hết x (tương tự)
5) 2x+8 chia hết 2x+1
=>(2x+8)-(2x+1) chia hết 2x+1
=> 2x+8-2x-1 chia hết 2x+1
=> 7 chia hết 2x+1 ( tương tự)
6) 2x+5 chia hết x+1
=> (2x+5) - 2(x+1) chia hết x + 1
=> 2x+5 - 2x - 2 chia hết x+1
=> 3 chia hết x+1
Nhấn đúng cho mk nha!!!!!!!!!!!!!!!!!
MA
29 tháng 1 2016
1) ta có 2x+5=2(x+2)+1
vì 2(x+2) chia hết cho x+2 nên để 2(x+2)+1 chia hết cho x+2 thì 1 chia hết cho x+2
hay x+2 là ước của 1
ta có Ư(1)=-1,1
nếu x+2=1 thì x=-1
nếu x+2=-1 thì x=-3
2) ta có 3x+5=3(x-2)+11
vì 3(x-2) chia hết cho x-2 nên để 3(x-2)+11 thì 11 chia hết cho x-2 hay x-2 là ước của 11
ta có Ư(11)=-11;-1;1;11
nếu x-2=-11 thì x=-9
nếu x-2=-1 thì x=1
nếu x-2=1 thì x=3
nếu x-2=11 thì x=12
các câu còn lại tương tự .cho mình **** nha
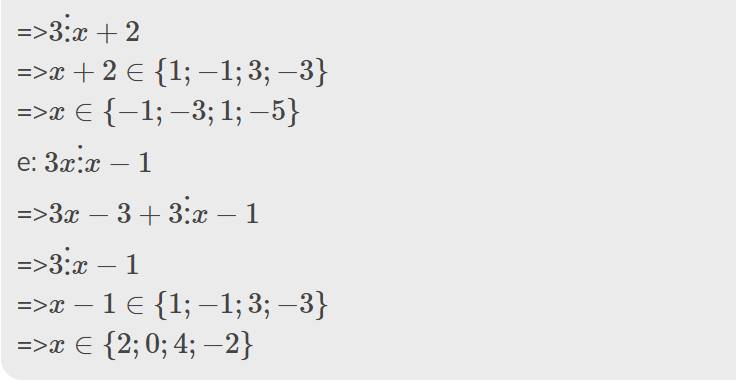
Bài 1
a) 6x + 4 chia hết cho 2x – 1.
6x + 4 - 3(2x - 1) chia hết cho 2x - 1
6x + 4 - 6x +3 chia hết cho 2x - 1
7 chia hết cho 2x - 1
⇒2x - 1 là Ư(7)={±1;±7}
Mà 2x - 1 chia 2 dư 1 hoặc -1
⇒ 2x - 1 ∈ {±1;±7}
⇒2x ∈ {-6;0;2;8}
⇒x ∈ {-3;0;1;4}
Vậy x ∈ {-3;0;1;4}
b, (-1) + 3 + (-5) + 7 + … + x = 600. (1)
Từ (1)⇒[(-1) + 3] + [(-5) + 7] + … +[-(x-2)+ x] = 600
Ta có : 2 + 2 + .........+ 2 =600
⇒2(1+1+......+1)=600
⇒1+1+....+1=300
Số dấu ngoặc là: x−34x−34 +1
⇒x−34x−34 +1=300⇒x=1199
Vậy x =1199
Bài 2
a,Để A đạt GTNN thì |x-9| + 2015 nhỏ nhất (1)
Mà |x-9| ≥ 0 ∀ x
⇒Để (1) xảy ra thì |x-9|=0⇒x-9=0⇒x=9
⇒GTNN của A=0+2015=2015
Vậy A đạt GTNN=2015 khi x =9
b,Để B đạt GTLN thì 5-|x+4| nhỏ nhất (2)
Mà |x+4| ≥ 0 ∀ x
⇒Để (2) xảy ra thì |x+4|=0⇒x+4=0⇒x= -4
⇒GTLN của B=5-0=5
Vậy B đạt GTLN=5 khi x = -4