Bài 1: TỪ một điểm M cố định bên ngoài dg tròn (O) ,kẻ một tiếp tuyến MT và một cát tuyến MAB của dg tròn đó
CM: MT^2= MA.MB
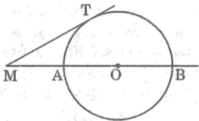
Bài 2: Cho nửa dg tròn (O) dg kính AB. Trên tia đối của tia AB lấy một điểm M vẽ tiếp tuyến MC với nửa dg tròn gọi là H là hình chiếu của C trên AB
a) CM: tam giác MAC đồng dạng tam giác MCB
b) CM :MA. MB=MO.MH
c) CM :CA là tia phân giác của góc MCH

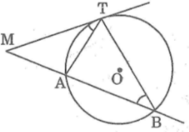

xét (o) có ^MTA là góc tạo bởi tt à dc chắn cung TA
^TBM là góc nt chắn cung TA
=> ^MTA = ^TBM (hq)
xét tg MTA và tg MBT có ^M chung
=> tg MTA đồng dạng tg MBT (g-g)
=> MT/MB = MA/MT
=> MT^2 = MB.MA
bài 2 tự kẻ hình đi
a, như bài 1
b, tg MAC đồng dạng tg MCB (câu a)
=> MA/MC = MC/MB
=> MC^2 = MA.MB (1)
xét tg MCO có ^MCO = 90 do MC là tt
CH _|_ MO
=> mc^2 = mh.mo (ĐL) (2)
(1)(2) => MH.MO = MA.MB
c, xét tg AHC và tg ACB có : ^ACB = ^AHC = 90(do C thuộc đường tròn đk AB)
^cah CHUNG
=> tg AHC đồng dạng tg ACB
=> ^ACH = ^CBA mà ^CBA = ^MCA (Câu a)
=> ^ACH = ^MCA
=> CA là pg...