Cho đường trong (O;R). Từ 1 điểm M nằm ngoài đường tròn vẽ 2 tiếp tuyến MA và MB (A:B là 2 tiếp điểm). Vẽ cát tuyến MCD với đường tròn (C nằm giữa M và D), gọi I là trung điểm của CD. Chứng minh A,B cùng nằm trên đường tròn đường kính OM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2015
mình cũng muốn giúp bạn lắm nhưng mới học lớp 6 nên chưa biết làm
CM
11 tháng 4 2018
Đáp án C
Phép vị tự tâm O tỉ số k biến tâm I 1 ; 2 của đường tròn (C) thành tâm I ' − 2, − 4 của đường tròn (C') bán kính bằng hai lần bán kính đường tròn C ' ⇒ P T C ' : x + 2 2 + y + 4 2 = 16
4 tháng 12 2023
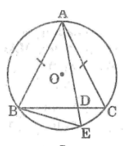
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(\widehat{BAC}=90^0\)
Xét ΔABC có
O là trung điểm của BC
OD//AC
Do đó: D là trung điểm của AB
b:
Ta có: ΔOAB cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)AB
=>OE\(\perp\)AB tại D
ΔOAB cân tại O
mà OE là đường cao(OE\(\perp\)AB tại D
nên OE là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOE}=\widehat{BOE}\)
Xét ΔOBE và ΔOAE có
OB=OA
\(\widehat{BOE}=\widehat{AOE}\)
OE chung
Do đó: ΔOBE=ΔOAE
=>\(\widehat{OBE}=\widehat{OAE}=90^0\)
=>EA là tiếp tuyến của (O)
c:Ta có: OE\(\perp\)AB
AB\(\perp\)AC
Do đó: OE//AC
Xét ΔFBC có
O là trung điểm của BC
OE//FC
Do đó: E là trung điểm của BF