giúp em câu b d c ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Thay \(x=\dfrac{1}{4}\) vào Q, ta được:
\(Q=\dfrac{1}{\dfrac{1}{4}\cdot\dfrac{1}{2}+27}=\dfrac{1}{27+\dfrac{1}{8}}=\dfrac{8}{217}\)
b) Ta có: \(P=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{1}{2-\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-9+\sqrt{x}+3-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(P>\dfrac{1}{2}\) thì \(P-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\left(\sqrt{x}+3\right)}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)

Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng



b) Ta có: \(\left(-\dfrac{1}{2}\right)^2\cdot2\dfrac{6}{7}-\dfrac{14}{15}:2\dfrac{1}{3}+\left(-1.21\right)^0\)
\(=\dfrac{1}{4}\cdot\dfrac{20}{7}-\dfrac{14}{15}:\dfrac{7}{3}+1\)
\(=\dfrac{5}{7}-\dfrac{14}{15}\cdot\dfrac{3}{7}+1\)
\(=\dfrac{5}{7}-\dfrac{2}{5}+1\)
\(=\dfrac{25-14-35}{35}=\dfrac{-24}{35}\)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`





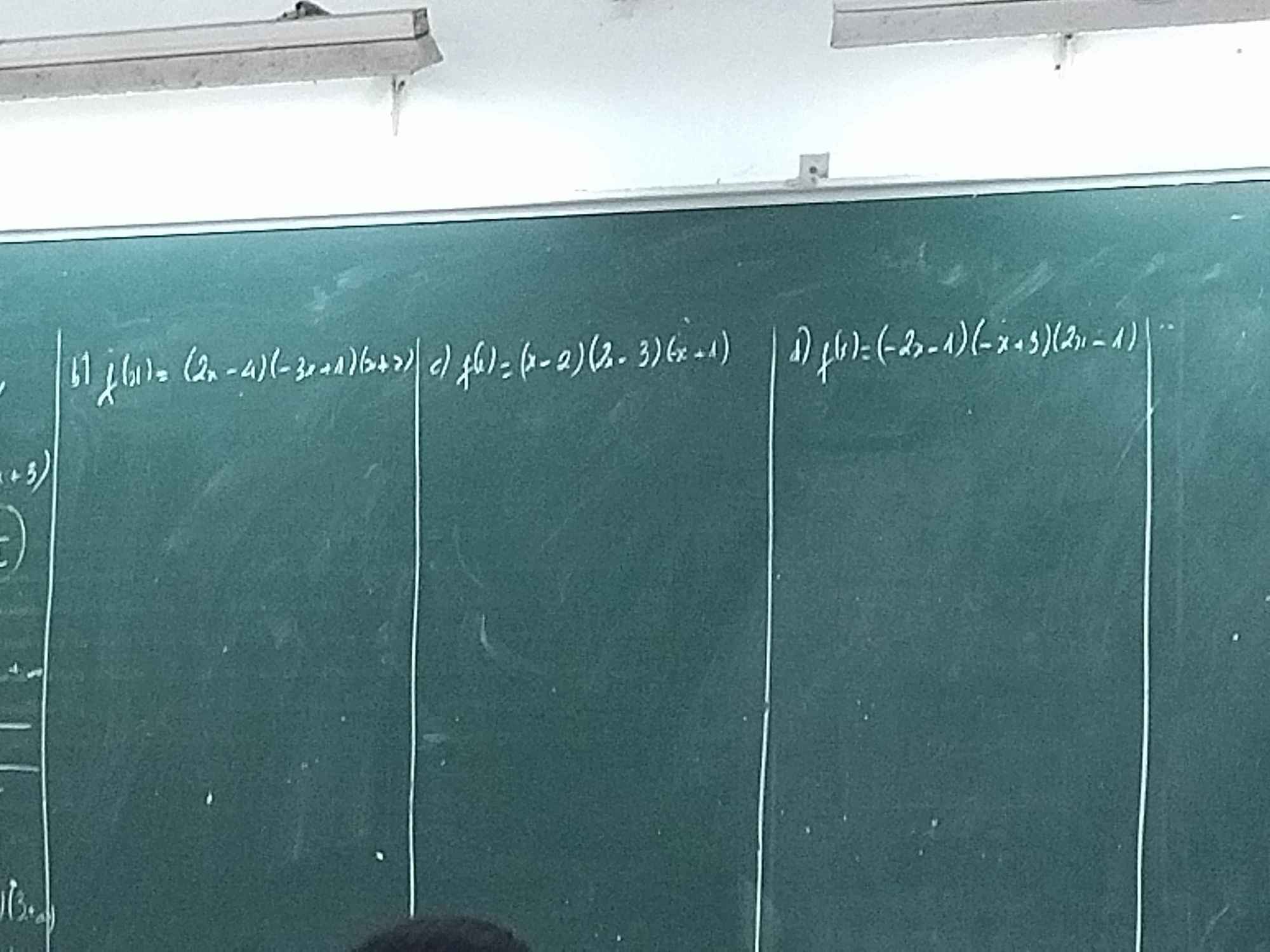
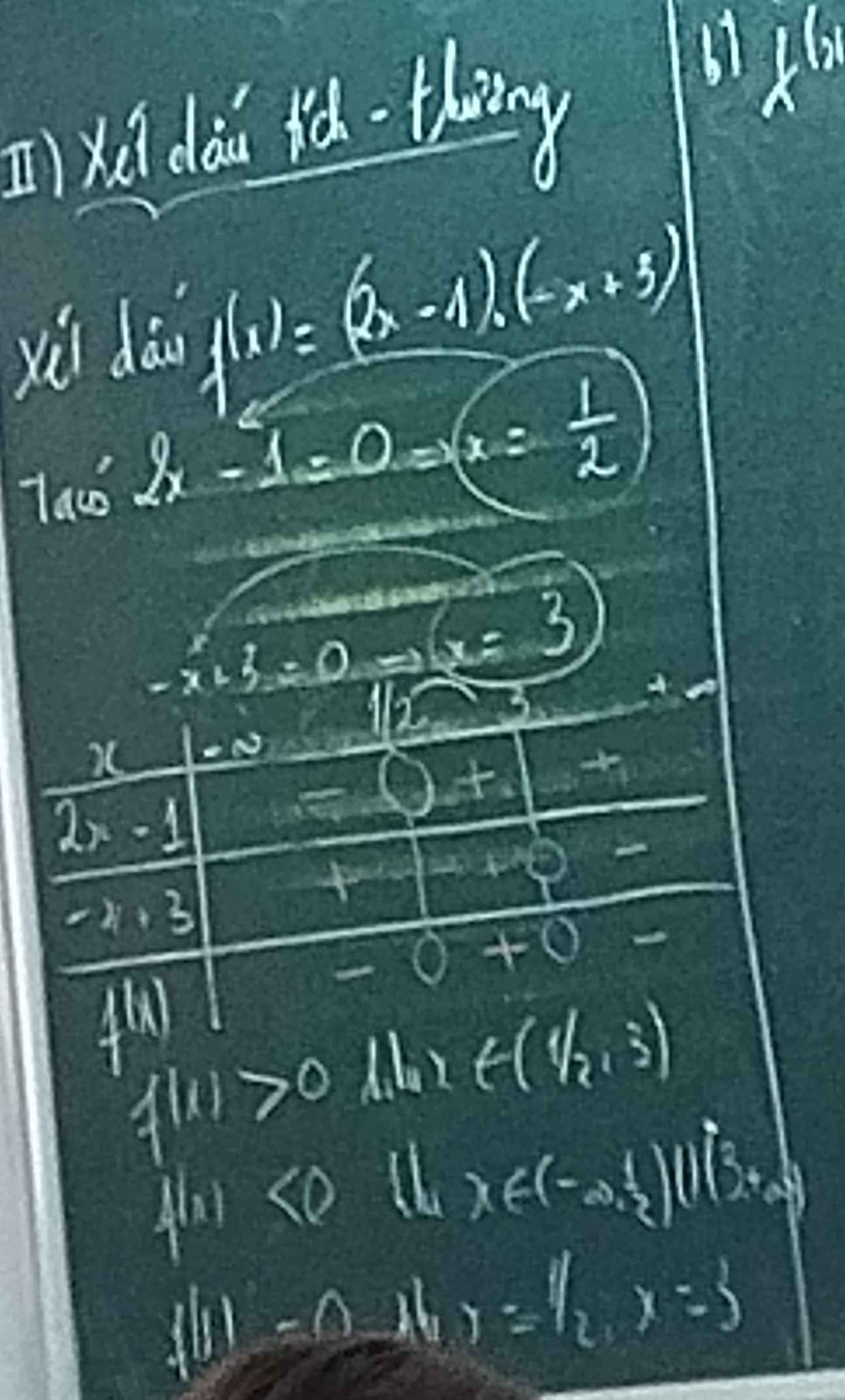
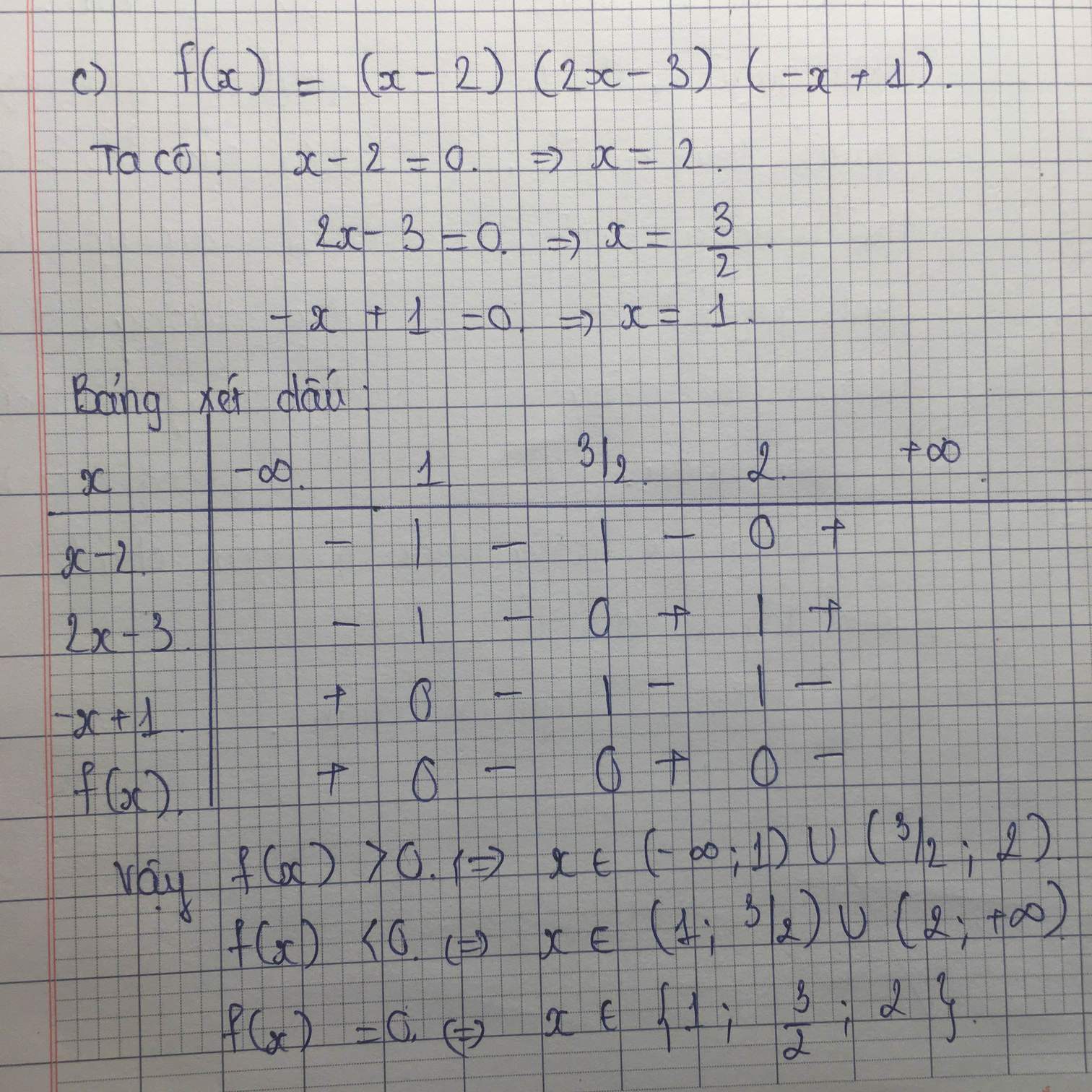

 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Ta có: \(\left\{{}\begin{matrix}x-y\sqrt{2}=6\\2\sqrt{2}x-3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3\sqrt{2}\cdot y=18\\4x-3\sqrt{2}\cdot y=8\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=18-8\sqrt{2}\\x-y\sqrt{2}=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y\sqrt{2}=x-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y\sqrt{2}=8\sqrt{2}-18-6=8\sqrt{2}-24\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y=8-12\sqrt{2}\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=8\sqrt{2}-18\\y=8-12\sqrt{2}\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}3x+2y=3\\5x+3y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x+10y=15\\15x+9y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-15\\3x+2y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=3-2y=3-2\cdot\left(-15\right)=33\\y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=11\\y=-15\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=11\\y=-15\end{matrix}\right.\)
d) Ta có: \(\left\{{}\begin{matrix}x-3y=23\\4x+5y=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-12y=92\\4x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-17y=85\\x-3y=23\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-5\\x=23+3y=23+3\cdot\left(-5\right)=8\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(8;-5)