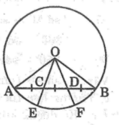
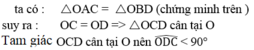Cho điểm A ở trong (O) và hai dây cung BC, EF. Chứng minh: AB . AC = AE . AF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2017
hình( tự vẽ)
a) Chú ý: \(\widehat{AEB}=\widehat{AFB}=90\)(góc chắn nửa đường tròn) => H là trực tâm tam giác ABC
=> tứ giác AIFC nội tiếp (do \(\widehat{AIC}=\widehat{AFC}=90\)) => góc CIF= góc CAF
mà góc CAF=\(\frac{1}{2}\)góc EOF
mà EF=R => tam giác OEF đều => EOF =60 => CIF=30
b)
tam giác vuông AIC đồng dạng với tam giác vuông AEB (g-g)
=> AE.AC=AI.AB
Tương tự tam giác BIC đồng dạng BFA
=> BF.BC=BI.AB
Vậy: AE.AC+BF.BC=AB(AI+IB)=AB\(^2\)=4R\(^2\)=const (ĐPCM)
5 tháng 1 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔABC có
AE/AB=AF/AC
Do đó: EF//BC
3 tháng 12 2023
Kẻ EM ⊥AH tại M,Kẻ FM ⊥AH tại M
Xét ∆MEA và ∆ vuông HAB có :
∠M = ∠N = 90^o
FA = AB
EAI = ABH
∆MEA = ∆HAB (ch - gn)
⇒ EM = AH (2 cạnh tương ứng)
Xét ∆NFA và ∆HAC ta có :
∠M = ∠N
AF = AC
∠FAN = ∠CAH
⇒ ∆NFA = ∆HAC (ch - gn)
⇒ EI = FN (2 cạnh tương ứng)
⇒ EM //FN (Vì EM ⊥AH tại M,Kẻ FM ⊥AH tại M)
⇒ MEO = NFO ( 2 so le trong)
Xét ∆MEO và ∆NFO ta có :
∠M = ∠N = 90^o
EM = FN (cmt)
∠MEO = ∠NFO (cmt)
⇒ ∆MEO = ∆NFO (ch - gn)
⇒ EO = FO
⇒O là trung điểm FE
