Viên đạn có khối lượng 1,3kg đang bay theo phương ngang với vận tốc 150m/s thì nổ thành 2 mảnh, mảnh thứ nhất có khối lượng 0,8kg bay hướng lên với vận tốc 112,5căn3 m/s và hợp với phương thẳng đứng một góc 600. Xác định hướng và độ lớn vận tốc của mảnh còn lại.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
4 tháng 10 2019
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng p → = p → 1 + p → 2
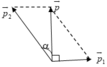
Với p = m v = 2.250 = 500 ( k g m / s ) p 1 = m 1 v 1 = 1.500 = 500 ( k g m / s ) p 2 = m 2 v 2 = v 2 ( k g m / s )
Vì
v → 1 ⊥ v → ⇒ p → 1 ⊥ p → t h e o p i t a g o ⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 ( k g m / s )
⇒ v 2 = p 2 = 500 2 ( m / s ) M à sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 0 với vận tốc 500 2 ( m / s )
VT
27 tháng 11 2018
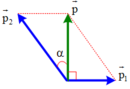
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 2.250 = 500 k g . m / s p 1 = m 1 v 1 = 1.500 = 500 k g . m / s p 2 = m 2 v 2 = v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 k g m / s
+ Mà sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 ° với vận tốc 500 2 m / s (m/s)
Chọn đáp án A
30 tháng 1 2021
Gọi \(\overrightarrow{v};\overrightarrow{v_1};\overrightarrow{v_2}\) lần lượt là vận tốc của viên đạn ban đầu, của mảnh đạn 1kg và mảnh đạn 2kg sau khi bắn
Động lượng ban đầu của viên đạn là
\(\overrightarrow{p_0}=3\overrightarrow{v}\)
Động lượng sau của hệ là
\(\overrightarrow{p_s}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
Do động lượng được bảo toàn nên
\(\overrightarrow{p_0}=\overrightarrow{p_s}\) ⇒ \(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(\overrightarrow{v_1}=3\overrightarrow{v}-2\overrightarrow{v_2}\)
⇒ v12 = 9.v2 + 4v22 - 12 . v . v2 . cos (45)
⇒ v12 = 9 . 472 + 4.502 - 12 . 47 . 50 . \(\dfrac{\sqrt{2}}{2}\)
⇒ v1 = 99,7 (m/s)
\(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(2\overrightarrow{v_2}=3\overrightarrow{v}-\overrightarrow{v_1}\)
⇒ cos \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 0.789
⇒ \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 37054'
Vậy mảnh đạn 1 bay theo chiều dương và hợp với phương thẳng đứng 1 góc 37054' có độ lớn là 99,7 m/s
28 tháng 2 2022
Tham khảo:
Giải thích các bước giải:
m=2kg;v=250m/s;v1=500m/s;α1=600
Bảo toàn động lượng của viên đạn trước và sau khi nổ:
P→=P1→+P2→
ta thấy:
P=m.v=2.250=500kg.m/s
P1=m1.v1=22.500=500kg.m/s
Theo quy tắc hình bình hành ta có:
(P1→;P2→)=600^;P1=P⇒P1=P2=P
Vận tốc mảnh thứ 2:
{P1=P2m1=m2
{P1=P2m1=m2
⇒v1=v2=500m/s
28 tháng 2 2022
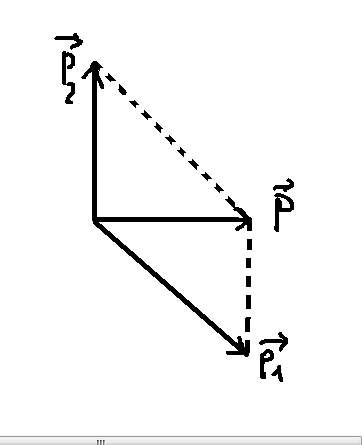
Bảo toàn động lượng: \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Quy tắc hình bình hành:
\(p_2^2=p_1^2+p^2-2p_1\cdot p\cdot cos\left(\overrightarrow{p_1};\overrightarrow{p}\right)\)
\(=\left(1\cdot500\right)^2+\left(2\cdot250\right)^2-2\cdot\left(1\cdot500\right)\cdot\left(2\cdot250\right)\cdot cos60^o\)
\(=250000\) \(\Rightarrow p_2=500kg.m\)/s
Mảnh thứ hai bay theo góc:
\(sin\alpha=\dfrac{p_1\cdot cos\left(90-30\right)}{p_2}=\dfrac{1\cdot250\cdot cos60}{500}=0,25\)
\(\Rightarrow\alpha\approx14,5^o\)
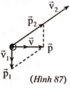
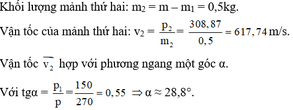
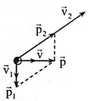
Xét hệ gồm 2 mảnh đạn trong thời gian nổ, đây là hệ kín nên ta áp dụng định luật bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p_h}\)
Trong đó: \(p_h=mv=195\left(kg.m/s\right)\)
\(p_1=m_1v_1=90\sqrt{3}\left(kg.m/s\right)\)
Áp dụng định lý hàm cos: \(p_2=\sqrt{p_1^2+p_h^2-2p_1p_h\cos\left(60^0\right)}\) => v2=p2/m2 =..... tự tính
Gọi \(\beta\) là góc hợp bởi phương ngang và mảnh thứ 2 ta có: \(\cos\beta=\dfrac{p_h^2+p_1^2-p_2^2}{2p_hp_1}=.......\) tự tính nốt :D
Học 10a3 Tân Thông Hội dk bạn