Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Động lượng của hệ là tổng động lượng của 2 vật có tính chất cùng phương ngược chiều nên ta
a) Vì \(\overrightarrow u = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).
Như vậy \(\overrightarrow u .\overrightarrow v = 0\)
Mặt khác: \(\overrightarrow u = \overrightarrow 0 \Leftrightarrow x = y = 0\)
\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)
b) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right)\end{array}\)
(|k|= k do k > 0)
c) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right).\end{array}\)
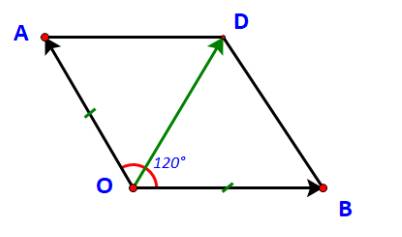
Gọi D là đỉnh thứ tư của hình bình hành OADB.
Khi đó ta có: \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} \)
Ta có: OA = OB = 120 suy ra tứ giác OADB là hình thoi
\( \Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}\)
\( \Rightarrow \Delta AOD\) đều (do OA = AD và \(\widehat {AOD} = {60^o}\))
\( \Rightarrow OD = OA = 120\)
Mặt khác: Do vật đứng yên nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = - (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = - \overrightarrow {OD} \)
Suy ra vecto \(\overrightarrow {OC} \) là vecto đối của vecto \(\overrightarrow {OD} \)
Lại có: \(\widehat {COA} = {180^o} - \widehat {AOD} = {120^o}\).Tương tự: \(\widehat {COB} = {120^o}\)
Vậy cường độ của lực \(\overrightarrow {{F_3}} \)là 120 N, tạo với lực\(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) góc \({120^o}\).
Định luật II Newton: \(\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\) (*)
Chiếu (*) lên trục xOy (Với Ox trùng với chiều chuyển động)
Oy: N=P
Ox: \(F-F_{ms}=ma\Leftrightarrow F-N\mu=ma\Leftrightarrow F-P\mu=ma\)
\(\Leftrightarrow F-mg\mu=ma\Leftrightarrow F=ma+mg\mu=1,6\left(N\right)\)
+ Chọn chiều dương Ox cùng chiều với v → 1
p = m 1 v 1 x + m 2 v 2 x = 2.5 + 5 − 2 = 0 k g . m / s
Chọn đáp án A
a, Động lượng của hệ: 
= 1 + 2
Độ lớn của hệ: p = p1 + p2 = m1v1 + m2v2 = 1.3 + 3.1 = 6 kg.m/s
b, Động lượng của hệ: = 1 + 2
Độ lớn của hệ: p = \(\left|p_1-p_2\right|=\left|m_1v_1-m_2v_2\right|=\left|3-3\right|\) = 0 kg.m/s
c, Động lượng của hệ : = 1 + 2
Độ lớn của hệ : p = \(\sqrt{p_1^2+p^2_2}=\sqrt{3^2+3^2}=\) 4,242 kg.m/s
d, Động lượng của hệ : = 1 + 2
Độ lớn của hệ : p = p1 = p2 = 3 kg.m/s
Đáp án A.
Chọn chiều dương Ox cùng chiều với v 1 →
p = m 1 v 1 x + m 2 v 2 x = 2.5 + 5 − 2 = 0 k g . m / s
Ph=P1+P2=6+4=10(kg.m/s) :D done