làm giúp mình bài 3 và 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2016
Đặt \(A=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}\)
\(3A=1+\frac{2}{3}+\frac{3}{3^2}+\frac{4}{3^3}+...+\frac{100}{3^{99}}\)
\(3A-A=\left(1+\frac{2}{3}+\frac{3}{3^2}+\frac{4}{3^3}+...+\frac{100}{3^{99}}\right)-\left(\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}\right)\)
\(2A=1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}}-\frac{100}{3^{100}}\)
\(6A=3+1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}}-\frac{100}{3^{99}}\)
\(6A-2A=\left(3+1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}}-\frac{100}{3^{99}}\right)-\left(1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}}-\frac{100}{3^{100}}\right)\)
\(4A=3-\frac{100}{3^{99}}-\frac{1}{3^{99}}+\frac{100}{3^{100}}\)
\(4A=3-\frac{300}{3^{100}}-\frac{3}{3^{100}}+\frac{100}{3^{100}}\)
\(4A=3-\frac{203}{3^{100}}< 3\)
\(A< \frac{3}{4}\left(đpcm\right)\)
- 1 số bài toán tương tự:
CMR: \(\frac{1}{4}+\frac{2}{4^2}+\frac{3}{4^3}+\frac{4}{4^4}+...+\frac{100}{4^{100}}< \frac{4}{9}\)
Dạng tổng quát: CMR: \(\frac{1}{k}+\frac{2}{k^2}+\frac{3}{k^3}+\frac{4}{k^4}+...+\frac{n}{k^n}< \frac{k}{\left(k-1\right)^2}\)(k;n \(\in\) N*; k > 1)
LN
0
DT
Đỗ Thanh Hải
CTVVIP
30 tháng 7 2021
các bạn khác k làm thì đừng cmt vô đây mấy bài của các bạn giải bị trôi
30 tháng 7 2021
1, \(\)BDT AM-GM
\(=>\sqrt{a^2+b^2}\ge\sqrt{2ab}\left(1\right)\)
tương tuqj \(=>\sqrt{b^2+c^2}\ge\sqrt{2bc}\left(2\right)\)
\(=>\sqrt{c^2+a^2}\ge\sqrt{2ac}\left(3\right)\)
cộng vế (1)(2)(3)
\(=>Vt=\sqrt{2}\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)=\sqrt{2021}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\dfrac{\sqrt{2021}}{\sqrt{2}}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\le a+b+c\)\(=>a+b+C\ge\dfrac{\sqrt{2021}}{\sqrt{2}}\)
đặt \(P=\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\)
\(=>P\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}=\dfrac{1}{2}.\dfrac{\sqrt{2021}}{\sqrt{2}}\)
dấu"=" xảy ra<=>\(a=b=c=\dfrac{\sqrt{2021}}{3\sqrt{2}}\)
(3-4 điểm thưởng/ý làm)
31 tháng 7 2021
C7, \(\dfrac{\left(b+c\right)\left(a^2+bc\right)}{b^2+bc+c^2}\ge\dfrac{\left(2\sqrt{bc}\right).\left(2a\sqrt{bc}\right)}{3\sqrt[3]{b^2.bc.c^2}}=\dfrac{4abc}{3abc}=\dfrac{4}{3}\left(1\right)\)
tương tự \(=>\dfrac{\left(a+c\right)\left(b^2+Ac\right)}{a^2+ac+c^2}\ge\dfrac{4}{3}\left(2\right)\)
\(=>\dfrac{\left(b+a\right)\left(c^2+ba\right)}{a^2+ab+b^2}\ge\dfrac{4}{3}\left(3\right)\)
cộng vế (1)(2)(3) \(=>P\ge4\)
dấu"=" xảy ra<=>a=b=c=1
BK
4
H9
HT.Phong (9A5)
CTVHS
6 tháng 3 2023
\(\dfrac{3}{4}-\dfrac{7}{5}+\dfrac{3}{10}\)
\(=\dfrac{15}{20}-\dfrac{28}{20}+\dfrac{6}{20}\)
\(=\dfrac{-7}{20}\)
BK
2
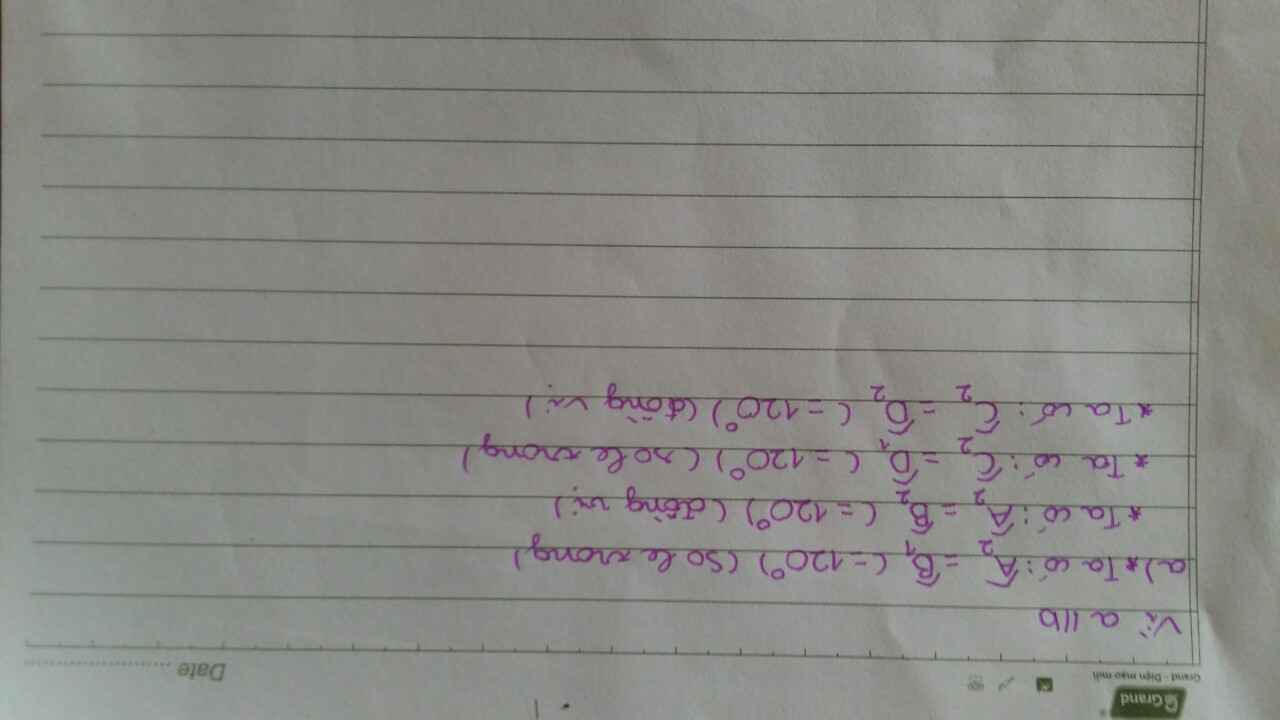
làm giúp mình bài 5 và 6
Bài 3:
a) Ta có: \(BC^2=25^2=625\)
\(AB^2+AC^2=20^2+15^2=625\)
Do đó: \(BC^2=AB^2+AC^2\)(=625)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=20^2-12^2=256\)
hay HB=16(cm)
Ta có: HB+HC=BC(H nằm giữa B và C)
\(\Leftrightarrow HC=BC-HB=25-16\)
hay HC=9(cm)
Vậy: HB=16cm; HC=9cm