Cho ΔABCcân tại A. Vẽ AE vuông góc với AB, AF vuông góc với AC sao cho EF // BC. Lấy trung điểm M của EF, chứng minh AM vuông góc với BC.
o l m . v n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này giống bài 33 phần TH bằng nhau thứ hai của tam giác trong sách Nâng cao và phát triển Toán 7 đó bn

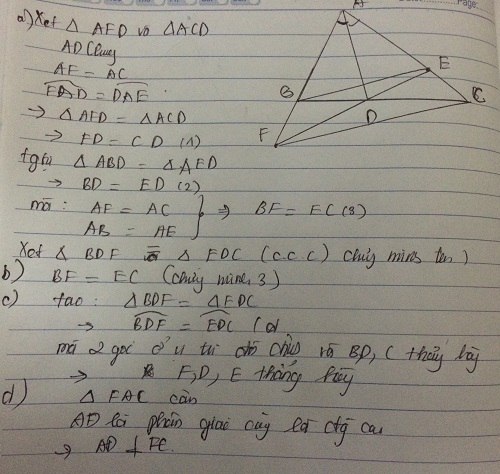
Đúng ko ben 10
Ai trên 10 điểm hỏi đáp thì mình nha mình đang cần gấp chỉ còn 60 điểm là tròn rồi mong các bạn hỗ trợ mình sẽ đền bù xứng đáng

b xem bài tương tự trong phần hình học nhé https://cunghocvui.com/danh-muc/toan-lop-7

Bạn tự vẽ hình nhé!
a) Xét tam giác vuông ABH có: góc ABH + BAH = 90o
Lại có: góc EAM + BAH = 90o (do góc EAB = 90o)
=> góc ABH = EAM
Xét tam giác vuông ABH và EAM có: góc ABH = EAM ; cạnh AB = EA
=> tam giác vuông ABH = EAM (cạnh huyền - góc nhọn)
=> BH = AM ;AH = EM
Ta có HM = AM + AH = BH + EM
Tương tự, tam giác vuông ANF = CHA => AN = CH; NF = HA
Ta có: HN = HA + AN = NF + CH
b) Ta có: EM = NF ( = cùng = HA)
góc IEM = IFN (2 góc So le trong do FN // EM)
Mà góc FNI = IME (= 90o)
=> tam giác INF = IME ( g- c - g)
=> IN = IM => I là trung điểm của EF

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF

a) ˆIAC=ˆBAK (=140o)IAC^=BAK^ (=140o)
ΔIAC=ΔBAKΔIAC=ΔBAK (c.g.c) ⇒IC=BK⇒IC=BK.
b) Gọi D là giao điểm của AB và IC, gọi E là giao điểm của IC và BK.
Xét ΔAIDΔAID và ΔEBDΔEBD, ta có ˆAID=ˆEBDAID^=EBD^ (do ΔIAC=ΔBAK)ΔIAC=ΔBAK), (đối đỉnh) nên ˆIAD=ˆBEDIAD^=BED^.
Do ˆIAD=90oIAD^=90o nên ˆBED=90oBED^=90o. Vậy IC⊥BKIC ⊥ BK.