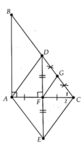
Cho ABC vuông tại A có . Gọi D, E lần lượt là trung điểm của các
cạnh BC và AC.
a/ Tính độ dài DE và AD, biết BC = 5cm, AC = 4cm.
b/ Lấy điểm F đối xứng với D qua AC, chứng minh rằng ADCF là hình thoi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
29 tháng 11 2021
a, Trong △ABC có:
D là trung điểm của BC, E là trung điểm của AC.
⇒ DE là đường trung bình của △ABC.
⇒ DE = 1/2AB (1)
và: DE // AB (2)
Từ (1) suy ra: DE = 1/2 . 6 = 3.
b, Ta có: F là điểm đối xứng với D qua E nên:
DE = DF
⇒ DF = 2DE = 2 . 1/2AB = AB (3) (theo (1)
Từ (2),(3) suy ra: ABDF là hình bình hành.
c, Do ABDF là hình bình hành nên:
AF // BD (4) và: AF = BD
Mặt khác, ta có: D là trung điểm của BC
=> BD = BC. Mà: AF = BD (cmt)
=> BC = AF (5).
Từ (4) và (5) suy ra: Tứ giác ADCF là hình bình hành.
Ta lại có: AB⊥AC (góc A = 90o)
và: AB // DF
⇒ AC⊥DF.
Vậy, hình bình hành ADCF có hai đường chéo vuông góc hay:
ADCF là hình thoi.
Ta có: ADCF là hình thoi ⇒AE = 1/2AC = 4.
Xét △ADE có: góc E = 90∘ (AC⊥DF)
⇒ AE2 + DE2 = AD2 (Định lý Pythagore)
thay số: 42 + 32 = AD2
16 + 9 = AD2
25 = AD2 => AD = 5 cm.
d, Để ADCF là hình vuông thì: AD⊥BC.
Mà: DC = DB = 1/2BC (gt) nên:
AD⊥BC khi và chỉ khi AD là đường trung trực của BC hay:
AB = AC
=> △ABC vuông cân tại A.
Vậy, điều kiện để ADCF là hình vuông là △ABC vuông cân tại A
7 tháng 1 2022
a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=20(cm)
Xét ΔABC có
D là trung điểm của BC
I là trung điểm của AB
Do đó: DI là đường trung bình
=>DI=AC/2=8(cm)
Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=BC/2=10(cm)
b: Xét tứ giác ABKC có
D là trung điểm của BC
D là trung điểm của AK
Do dó: ABKC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABKC là hình chữ nhật
c: Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
17 tháng 10 2016
a, △ABC có: là trung điểm của BC, là trung điểm của
⇒DE là đường trung bình của
b, Có: F là điểm đối xứng với D qua E
(theo (2),(3)⇒ABDF là hình bình hành ◻
c, ABDF là hình bình hành
Mặt khác là trung điểm của nên
(4),(5)⇒ADCF là hình bình hành
Ta lại có: AB//DF⇒AC⊥DF
Vậy hình bình hành có hai đường chéo vuông góc hay là là hình thoi
Có là hình thoi
có (AC⊥DF)
(Định lý Pythagore)
thay AE=4 và DE=3 tính được
d, Để là hình vuông thì
Mà có nên khi và chỉ khi là đường trung trực của
Tức là hay vuông cân tại A
Điều kiện để là hình vuông là vuông cân tại A
sai thì thôi nha
15 tháng 3 2020
Giải thích các bước giải:
ta có: Tam giác ABC vuông tại A (gt)
=> AB^2+AC^2=BC^2
6^2+8^2 =BC^2
36+64 =BC^2
100 =BC^2
=>BC=10cm
Tam giác ABC vuông tại A có Am là đg trung tuyến
=> AM=BC/2=10/2=5cm
15 tháng 3 2020
HÌNH VẼ THÌ BẠN TỰ VẼ NHÉ, HÌNH NÀY DỄ VẼ MÀ NHỈ.
Câu a bạn V (Team BTS) làm rồi nên mình chỉ làm các câu còn lại thôi nhé.
b) Vì DM vuông góc AB, AC vuông góc AB (gt) => DM // AC.
=> DMCA là hình thang mà góc ADM = góc DAC = 90 độ.
Do đó ADMC là hình thang vuông.
c) Xét tam giác ABC ta có: DM // AC (cmt), M là trung điểm BC (AM là trung tuyến)
=> D là trung điểm của AB.
Tứ giác AEBM có AB và EM là hai đường chéo cắt nhau tại trung điểm D. => AEBM là hình bình hành. (1)
Lại xét tam giác AMB cân tại M (MA=MB) có MD là trung tuyến => MD cũng là đường cao=> ME vuông góc AB tại D. (2)
Từ (1) và (2) => AEBM là hình thoi.
d) Vì AEBM là hình thoi => AE // BM, AE = BM.
Mà BM = MC => AE // MC, AE = MC. Do đó AEMC là hình bình hành.
e, Câu e mình không hiểu lắm vì thấy đề bài cứ sai sai làm sao. Mình chỉ chứng minh câu F đối xứng với E qua A thôi nhé.
Gọi I là giao điểm của AC và MF. Vì M đối xứng F qua AC => I là trung điểm MF, AC vuông góc MF tại I.
Chứng minh tương tự câu c ta sẽ được AFMC là hình thoi => AF // MC, AF = MC.
Mà AE // MC, AE = MC (cmt)
=> A, E, F thẳng hàng (tiên đề Ơ-clit) và A là trung điểm của EF (AE=AF)
Vậy F đối xứng E qua A.
31 tháng 10 2021
a: Ta có: I và D đối xứng nhau qua AB
nên AB là đường trung trực của DI
Suy ra: AD=AI
hay AB là tia phân giác của \(\widehat{IAD}\)
Ta có: I và E đối xứng nhau qua AC
nên AC là đường trung trực của IE
Suy ra: AI=AE
hay AC là tia phân giác của \(\widehat{EAI}\)
Ta có: \(\widehat{EAD}=\widehat{EAI}+\widehat{DAI}\)
\(=2\left(\widehat{BAI}+\widehat{CAI}\right)\)
\(=2\cdot90^0=180^0\)
Suy ra:E,A,D thẳng hàng
mà AD=AE(=AI)
nên A là trung điểm của DE
CM
30 tháng 12 2017
a) Ta có AD = 1 2 B C = 8 2 = 4 c m
Xét DADC có GF là đường trung bình
⇒ G F = 1 2 A D = 4 2 = 2 c m
b) Chứng minh ADCE là hình thoi. Để ADCE là hình vuông thì điều kiện cần và đủ là E C D ^ = 90 0 ⇔ C 1 ^ = C 2 ^ = 45 0
Û DABC vuông tại A.
