25-y2=2020(x-2019)2.Tìm x, y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì x,y nguyên \(\Rightarrow2020\left(x-2019\right)^2>2020\left(x\ne0\right)\)
mà \(25^2-y^2\le25^2=625\)
Theo bài ra : \(2020\left(x-2019\right)^2=25-y^2\)
Vậy x=0 vì \(x\ne0\)thì 2020(x-2019)2>2020
Thay x=0 vào pt:
25-y2=0=> y= 5 hoặc y=-5

a) Ta có:\(8\left(x-2019\right)^2⋮8\Rightarrow25-y^2⋮8\)\(\left(1\right)\)
Mặt khác: \(8\left(x-2019\right)^2\ge0\Rightarrow25-y^2\ge0\)\(\left(2\right)\)
Từ\(\left(1\right),\left(2\right)\)ta có: \(y^2=1;9;25\)
Xét:\(y^2=1\Rightarrow8\left(x-2019\right)^2=24\Rightarrow\left(x-2019\right)^2=3\left(ktm\right)\)
\(y^2=9\Rightarrow8\left(x-2019\right)^2=16\Rightarrow\left(x-2019\right)^2=2\left(ktm\right)\)
\(y^2=25\Rightarrow8\left(x-2019\right)^2=0\Rightarrow\left(x-2019\right)^2=0\Rightarrow x-2019=0\Rightarrow x=2019\left(tm\right)\)
Vậy \(y=5;x=2019\)
\(y=-5;x=2019\)

\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)

a) (y + 5) x 2020 = 205 x 2020
(y + 5) x 2020 = 414100
y + 5 = 414100 : 2020 = 205
y = 205 - 5 = 200
a) y= 200
b) y-45600 = 1600 × 4 ×25
y-45600=160000
y= 114400

Ta có vế phải không âm nên vế trái không âm tức là \(y^2\le25\Leftrightarrow-5\le y\le5\)
Mặt khác thì vế phải chia hết cho 5 nên vế trái chia hết cho 5,suy ra y={-5;0;5}
+)Với y=-5 =>2020(x-2019)2=0=>x=2019
+)Với y=0=> 2020(x-2019)2=25,trường hợp này không tìm được x
+)Với y=-5 thì 2020(x-2019)2=0=>x=2019
Vậy giá trị thỏa mãn của (x;y) là (2019;5);(2019;-5)


\(25-y^2=2020\left(x-2019\right)^2\)
\(\frac{25-y^2}{2020}=\left(x-2019\right)^2\)
\(\pm\sqrt{\frac{25-y^2}{2020}}=x-2019\)
\(x-2019=\pm\sqrt{\frac{25-y^2}{2020}}\)
\(x-2019=\orbr{\begin{cases}\sqrt{\frac{25-y^2}{2020}}\\-\sqrt{\frac{25-y^2}{2020}}\end{cases}}\)
\(x=-\sqrt{\frac{25-y^2}{2020}}+2019\)
\(x=\sqrt{\frac{25-y^2}{2020}}+2019;-\sqrt{\frac{25-y^2}{2020}}+2019\)
=> ko ra :v
có y2\(\ge\)0
Nên 25-y2\(\le\)25
Vậy 2020(x-2019)2\(\le\)25
(x-2019)2\(\le\)\(\frac{5}{404}\)<1
=>x-2019\(\le\)0 => x=2019
Thay x=2019 vào đẳng thức
=> 25-y2=2020(2019-2019)2
25-y2=0
y2=25
Vậy y=5
\(\le\)

Cho a,b,c khác 0 t/m:
1/a+1/b+1/c=1/2018 và a+b+c=2018
cmr" 1/a^2019+1/b^2019+1/c^2019=1/(a^2019+b^2019+c^2019)
Ta có :
gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3
Đến đây là dạng của phương trình ước số bạn chỉ cần xét ước của 33 là sẽ tìm được nghiệm nguyên của PT

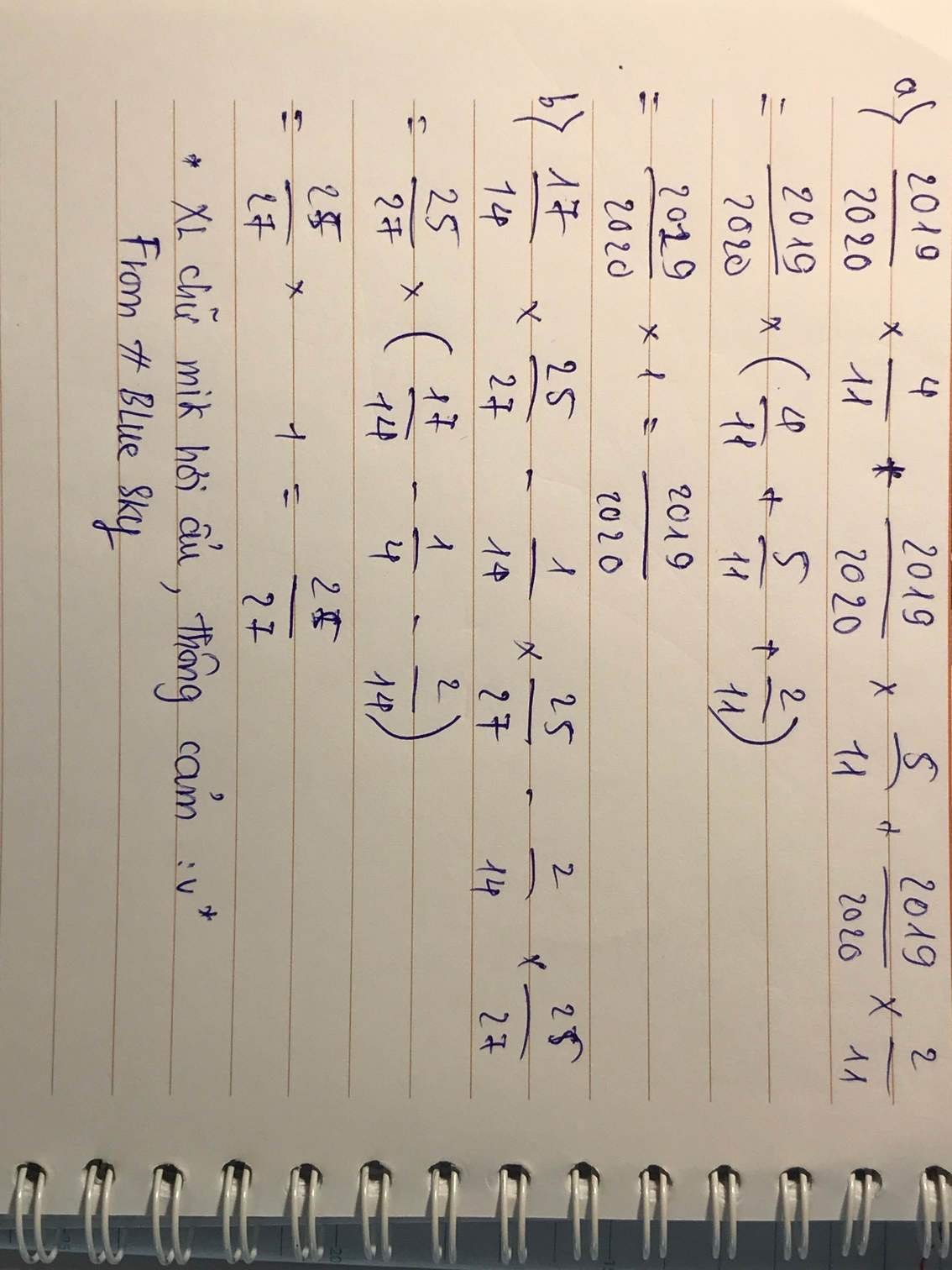
Ta có: 2020(x-2019)^2 >=0
=> 25-y^2 >=0 (1)
Lại có 2020(x-2019)^2 chia hết cho 2020 => 25-y^2 chia hết cho 2020 (2)
Mặt khác y^2>=0 =>25-y^2<=25 (3)
Từ(1),(2),(3) =>25-y^2=0 <=> y= 5 hoặc -5
Khi này : 2020(x-2019)^2=0 <=> x=2019
Vậy x=2019;y = 5 hoặc -5