2xy2-10x+y2=17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2021
a: \(=\left(3-x\right)\left(x+1\right)\)
b: \(=3x\left(x-y\right)-5\left(x-y\right)\)
=(x-y)(3x-5)
c: \(=x\left(x-y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)\left(x-10\right)\)
26 tháng 10 2021
a) \(=x\left(3-x\right)+\left(3-x\right)=\left(3-x\right)\left(x+3\right)\)
b) \(=3x\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(3x-5\right)\)
c) \(=x\left(x-y\right)-10\left(x-y\right)=\left(x-y\right)\left(x-10\right)\)
d) \(=\left(x+y\right)^2-16=\left(x+y-4\right)\left(x+y+4\right)\)
e) \(=\left(x-y\right)\left(x+y\right)-4\left(x+y\right)=\left(x+y\right)\left(x-y-4\right)\)
f) \(=9-\left(4x^2-4xy+y^2\right)=9-\left(2x-y\right)^2=\left(3-2x+y\right)\left(3+2x-y\right)\)
g) \(=y\left(y^2-2xy+x^2-y\right)\)
h) \(=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x^2-4\right)=\left(x-3\right)\left(x-2\right)\left(x+2\right)\)
i) \(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)=\left(x-y\right)\left(2x+y\right)\)
28 tháng 10 2021
\(A=x^2\left(x+y\right)+y^2\left(x+y\right)+2xy\left(x+y\right)\\ A=\left(x+y\right)\left(x^2+2xy+y^2\right)=\left(x+y\right)\left(x+y\right)^2\\ A=\left(x+y\right)^3\)
PT
1
14 tháng 11 2021
\(VT=\dfrac{2x^2+2xy+xy+y^2}{x^2\left(2x+y\right)-y^2\left(2x+y\right)}=\dfrac{2x\left(x+y\right)+y\left(x+y\right)}{\left(x^2-y^2\right)\left(2x+y\right)}\\ =\dfrac{\left(2x+y\right)\left(x+y\right)}{\left(2x+y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}=VP\)
NT
2
H9
HT.Phong (9A5)
CTVHS
24 tháng 7 2023
\(\left(2xy^2-5y^3\right):y^2+\left(12xy+6x^2\right):3x\)
\(=\dfrac{y^2\left(2x-5y\right)}{y^2}+\dfrac{3x\left(4y+2x\right)}{3x}\)
\(=2x-5y+4y+2x\)
\(=4x-y\)
Thay x=-3, y=-12 vào biểu thức ta có:
\(4\cdot-3-\left(-12\right)=0\)
Vậy: ...
24 tháng 7 2023
\(A=\dfrac{2xy^2-5y^3}{5y}+\dfrac{12xy+6x^2}{3x}\)
=2/5xy-y^2+4y+2x
Khi x=-3 và y=-12 thì A=2/5*(-3)*(-12)-144+4*(-12)+2*(-3)
=-183,6
21 tháng 10 2023
a: Sửa đề: \(2A+\left(2x^2+y^2\right)=6x^2+5y^2-2x^2y^2\)
=>\(2A=6x^2+5y^2-2x^2y^2-2x^2-y^2\)
=>\(2A=4x^2+4y^2-2x^2y^2\)
=>\(A=2x^2+2y^2-x^2y^2\)
b: \(2A-\left(xy+3x^2-2y^2\right)=x^2-8y+xy\)
=>\(2A=x^2-8y+xy+xy+3x^2-2y^2\)
=>\(2A=4x^2+2xy-8y-2y^2\)
=>\(A=2x^2+xy-4y-y^2\)
c: Sửa đề: \(A+\left(3x^2y-2xy^2\right)=2x^2y+4xy^3\)
=>\(A=2x^2y+4xy^3-3x^2y+2xy^2\)
=>\(A=-x^2y+4xy^3+2xy^2\)
xy
13 tháng 3 2022
rong các biểu thức sau, biểu thức nào là đơn thức ?
A. (x+y2 )z B. x/2-z C. – 5x + 1 D. (- 2xy2)
13 tháng 3 2022
Trong các biểu thức sau, biểu thức nào là đơn thức ?
A. (x+y2 )z B. x/2-z C. – 5x + 1 D. (- 2xy2)1/3xy2
20 tháng 12 2022
1:=x^3-27-x^2-3=x^3-x^2-30
2: =x-2+125x^3+150x^2+60x+8
=125x^3+150x^2+61x+6
3: \(=2xy-5y+5y=2xy\)
4: =25x-10x^2+15x
=-10x^2+40x
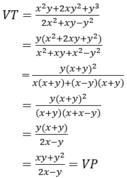
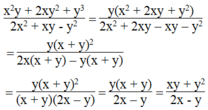
2xy^2-10x+y^2=17
(2xy^2+y^2) - (10x+5)=12
y^2(2x+1)-5(2x+1)=12
(2x+1)(y^2-5)=12
Mà x,y nguyên => 2x+1 là số lẻ; y^2-5 là số nguyên
Ta có bảng sau:
Kết luận : tồn tại 4 cặp giá trị x,y thỏa mãn