1. Giải các bất phương trình sau:

2. Gọi I, J lần lượt là trung điểm các cạnh AB, CD của tứ giác ABCD. Gọi G là trung điểm của đoạn thẳng IJ.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: vecto AC+vecto BD
=vecto AI+vecto IC+vecto BI+vecto ID
=vecto ID+vecto IC
=2*vecto IJ
vecto AD+vecto BC
=vecto AI+vecto ID+vecto BI+vecto IC
=vecto IC+vecto ID
=2*vecto IJ
=vecto AC+vecto BD
b: vecto GA+vecto GB+vecto GC+vecto GD
=2*vecto GI+2*vecto GJ
=2(vecto GI+vecto GJ)
=vecto 0

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

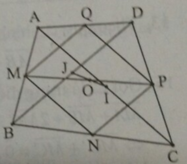
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
P là trung điểm của CD
N là trung điểm của BC
Do đó: PN là đường trung bình của ΔABD
Suy ra: PN//BD và \(PN=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//PN và MQ=PN
hay MNPQ là hình bình hành

Ta co:IA =IB(gt) ; HA =HC(gt)
Suy ra:HI la` đg tb của tam giac ABC
Suy ra:IH =1/2BC ;IH//BC (1)
Trong tam giac BDC co:KD =KB(gt) ;JD =JC(gt)
Suy ra :KJ la đg tb cu`a tam giac BDC
Suy ra :KJ =1/2BC ;KJ//BC (2)
Tu (1) va (2) suy ra :KJ = IH ;KJ // IH
Suy ra :tu giac KIHJ la hinh binh hanh(2 canh doi song song va bang nhau)(*)
Trong tam giac ADC co:HA =HC(gt) ;JD = JC(gt)
Suy ra :HJ la đg tb của tam giac ADC
Suy ra :HJ = 1/2AD
Mà AD =BC(gt) ; HI = 1/2BC(c/m tren)
Suy ra :HJ = HI (**)
Tu (*) va (**) suy ra tu giac KIHJ la hinh thoi (hbh co 2 canh ke bang nhau)
Suy ra :IJ vuong goc voi KH

+) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Từ đó suy ra: IJ // BC (3) .
- Từ (1) và (3) suy ra: MN // IJ .
→ Vậy tứ giác MNJI là hình thang.
+) Để MNJI là hình bình hành thì: MI// NJ.
- Lại có ba mặt phẳng (MNJI); (ABD); (ACD) đôi một cắt nhau theo các giao tuyến là MI, NJ, AD nên theo định lý 1 ta có: MI // AD // NJ (4)
- Mà I; J lần lượt là trung điểm BD,CD (5)
- Từ (4)và (5) suy ra: M, N lần lượt là trung điểm của AB, AC.
⇒ Vậy điều kiện để hình thang MNJI trở thành hình bình hành là M, N lần lượt là trung điểm của AB, AC.
a)Ta có:(x-2)(2x+1)<0
TH1:x-2<0 và 2x+1>0
Suy ra x<2 và x>-1/2 hay -1/2<x<2
TH2:x-2>0 và 2x+1<0
Suy ra x>2 và x<-1/2(vô lý)
Vậy -1/2<x<2
b)Ta có:(4x+5)2>0
Suy ra 4x+5 khác 0 hay x khác -5/4
Vậy x khác -5/4
c)Ta có:(x-3)(x+2)<=0
TH1:x-3<=0 và x+2>=0 hay -2<=x<=3
TH2:x-3>=0 và x+2<=0(vô lý)
Vậy -2<=x<=3
d)Ta có delta của pt=-32<0
Vậy bất phương trình nghiệm đúng với mọi x
e)TH1:(x-1)(3-2x)<0 và 2x-4<0 hay x<1 hoặc x>3/2 và x<2 hay x<1 hoặc 3/2<x<2
TH2:(x-1)(3-2x)>0 và 2x-4>0 hay 1<x<3/2 và x>2(vô lý)
Vậy x<1 hoặc 3/2<x<2
f)Ta có:5/(2x-1)-2/(x-1)<0 hay x-3/(2x-1)(x-1)<=0
TH1:x-3<=0 và (2x-1)(x-1)>0 hay 1<x<=3 hoặc x<=3
TH2:x-3>=0 và (2x-1)(x-1)<0 hay x>=3 và 1/2<x<1(vô lý)
g)Ta có:(-x2+2x+2)/(x-1)<=0
TH1:-x2+2x+2<=0 và x-1>0 hay x>1+căn 3
TH2:-x2+2x+2>=0 và x-1<0 hay 1-căn 3<x<1