Cho đường tròn (O), đg kính AB = 2R. Gọi d1 và d2 là 2 tiếp tuyến của đg tròn tâm O tại 2 điểm A và B. Gọi I là trung điểm của OA và E là điểm thuộc đường tròn tâm O (E không trùng với A và B). Đường thẳng d đi qua điểm E và vuông góc với EI cắt 2 đường thẳng d1 và d2 lần lượt tại M và N. C/m:a, AMEI là tứ giác nội tiếp.b, \(\widehat{ENI}\)= \(\widehat{EBI}\)và \(\widehat{MIN}\)= 90 độc,...
Đọc tiếp
Cho đường tròn (O), đg kính AB = 2R. Gọi d1 và d2 là 2 tiếp tuyến của đg tròn tâm O tại 2 điểm A và B. Gọi I là trung điểm của OA và E là điểm thuộc đường tròn tâm O (E không trùng với A và B). Đường thẳng d đi qua điểm E và vuông góc với EI cắt 2 đường thẳng d1 và d2 lần lượt tại M và N. C/m:
a, AMEI là tứ giác nội tiếp.
b, \(\widehat{ENI}\)= \(\widehat{EBI}\)và \(\widehat{MIN}\)= 90 độ
c, AM.BN=AI.BI
d, Gọi F là điểm chính giữa của cung AB không chứa E của đường tròn (O). Hãy tính diện tích của tam giác MIN theo R khi 3 điểm E,I,F thẳng hàng.
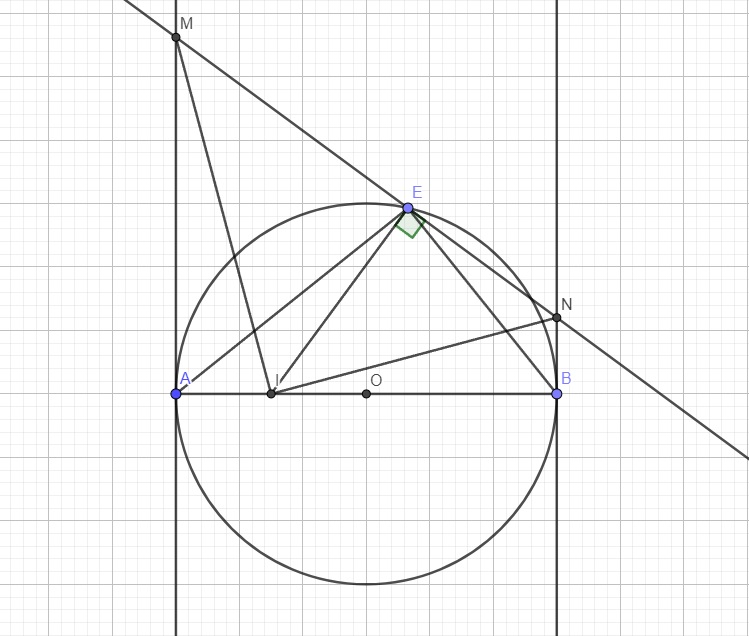
a,: ˆMAI+ˆMEI=180oMAI^+MEI^=180o => tứ giác AMEIAMEI nội tiếp
b, tương tự tứ giác EIBNEIBN nội tiếp =>ˆENI=ˆEIB(=12sdEI)ENI^=EIB^(=12sdEI);
ˆEIN=ˆEBN=12sđEB(1)EIN^=EBN^=12sđEB(1)
tứ guacs AMEIAMEI nội tiếp => ˆMIE=ˆMAE=12sđEA(2)MIE^=MAE^=12sđEA(2)
Từ (1) và (2) =>ˆMIN=12sđAB=90o=>MIN^=12sđAB=90o
c, ΔAMI ΔBIN(.....)ΔAMI ΔBIN(.....)
=>AMBI=AIBN=>=>AMBI=AIBN=> đpcm