Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Do khoảng thời gian ∆t thì xe chuyển động được quãng đường ∆s=v0.∆t=20∆t
Do đó, khi người lái xe bắt đầu hãm phanh thì khoảng cách giữa xe và chướng ngại vật là: s = 100 - 20∆Mà khi xe bị hãm phanh thì quãng đường xe còn chuyển động được đến khi dừng hẳn là:
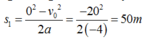
Vậy để xe không va vào chướng ngại vật thì
![]()
![]()

Có : \(\Delta W\)đ \(=\dfrac{1}{2}m\left(v^2_2-v_1^2\right)=\dfrac{1}{2}m.-225=-112,5m\left(J\right)\)
- Theo định lý biến thiên động năng :
\(\Delta W=A=Fs=mgs=-112,5m\)
\(\Rightarrow s=11,25\left(m\right)< 12\left(m\right)\)
Vậy xe không đâm vào chướng ngại vật .

Công lực hãm:
\(A_{hãm}=F_{hãm}\cdot s=8000\cdot10=80000J\)
\(v=36\)km/h=10m/s
Động năng ô tô va vào chướng ngại vật:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot4\cdot1000\cdot10^2=200000J\)
Vận tốc ô tô khi va vào chướng ngại vật là:
Bảo toàn động năng:
\(A_{hãm}=\Delta W=W_2-W_1\)
\(\Rightarrow W_2=W_1+A_{hãm}=200000+80000=280000J\)
Mà \(W_2=\dfrac{1}{2}mv'^2\Rightarrow v'=2\sqrt{35}\)m/s

Em có thể truy cập vào trang Scratch.mit.edu để xem và chơi các trò chơi được chia sẻ trên internet.


- Gọi số lần vượt qua chướng ngại vật và số lần va chạm là x và y ( số lần, x , y > 0 )
Theo bài ra trên đường chạy có tất cả 20 chướng ngại vật .
Nên ta có phương trình : \(x+y=20\) ( I )
- Số điểm bị trừ của 2 chị em là : \(1,5y\) ( điểm )
- Số điểm được thưởng của hai chị em là : \(2x\) ( điểm )
Mà để tổng số điểm lớn hơn 5 thì :
\(2x-1,5y>5\)
- Từ PT ( I ) ta được x = 20 - y
=> \(2\left(20-y\right)-1,5y>5\)
\(\Rightarrow40-3,5y>5\)
\(\Rightarrow y< 10\)
Mà hai chị em đã va chạm 6 lần .
Vậy để số điểm hơn 5 thì hai chị em chỉ được va chạm thêm 3 lần nữa .
mình cảm ơn nhiều 🥰