c) x 2 + ( m + 1 ) x + 2 m + 7 ≤ 0 vô nghiệm
Tìm m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kiểm tra giúp mình yêu cầu thứ nhất nhé!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (m2-1)x+2=m-1 nhận x=2 là nghiệm.
Giải: Thế x=2 vào phương trình đã cho, ta suy ra (m2-1).2+2=m-1 (vô nghiệm).
Không có giá trị nào của m để phương trình đã cho nhận x=2 là nghiệm. -Hết-".
Thế x=-1 vào phương trình đã cho, ta suy ra 3.(-1)2+4m.(-1)=8 \(\Rightarrow\) m=-5/4.
Bạn xem giúp mình yêu cầu cuối cùng nha!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (2m+3)x-5=(m+2)-x có nghiệm là x=3.
Giải: Thế x=3 vào phương trình đã cho, ta suy ra (2m+3).3-5=(m+2)-3 \(\Rightarrow\) m=-1. -Hết-".

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Chọn A.
ĐK: ![]()
TH1: m = 0: ![]()

TH2:
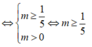
Vậy BPT đã cho vô nghiệm khi m ≥ 1 5

a.
Khi \(m=2\) pt trở thành:
\(2x+3=0\Rightarrow x=-\dfrac{3}{2}\)
b.
Để pt có nghiệm \(x=-1\)
\(\Rightarrow\left(m^2-m\right).\left(-1\right)+m^2-1=0\)
\(\Leftrightarrow-m^2+m+m^2-1=0\)
\(\Leftrightarrow m-1=0\)
\(\Leftrightarrow m=1\)
c.
Pt tương đương:
\(\left(m^2-m\right)x=-\left(m^2-1\right)\)
\(\Leftrightarrow m\left(m-1\right)x=-\left(m-1\right)\left(m+1\right)\)
Pt vô nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow m=0\)
\(\Rightarrow\) pt có nghiệm khi \(m\ne0\)
Pt có vô số nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)=0\end{matrix}\right.\) \(\Leftrightarrow m=1\)
Lời giải:
a. Khi $m=2$ thì pt trở thành:
$2x+3=0\Leftrightarrow x=-\frac{3}{2}$
b. Để pt có nghiệm $x=-1$ thì:
$(m^2-m).(-1)+m^2-1=0$
$\Leftrightarrow m-1=0\Leftrightarrow m=1$
c.
PT $\Leftrightarrow (m^2-m)x=1-m^2$
Để pt vô nghiệm thì: \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-1)=0\\ (1-m)(1+m)\neq 0\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
PT có vô số nghiệm khi \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2= 0\end{matrix}\right.\Leftrightarrow m=1\)
Để PT có nghiệm thì: $m\neq 0$

a, Để pt có 2 nghiệm pb khi \(\Delta>0\)
\(\Delta=\left(-2m\right)^2-4\left(m+6\right)=4m^2-4m-24>0\Leftrightarrow m< -2;m>3\)
b, Để pt trên là pt bậc 2 khi \(m\ne0\)
Để pt vô nghiệm khi \(\Delta< 0\)
\(\Delta=4m^2-4m\left(m+3\right)=4m^2-4m^2-12m< 0\Leftrightarrow-12m< 0\Leftrightarrow m>0\)
c, Để pt trên là pt bậc 2 khi \(m\ne2\)
Để pt trên có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m-3\right)^2-4\left(m+1\right)\left(m-2\right)=4m^2-12m+9-4\left(m^2-m-2\right)\)
\(=-8m+17=0\Leftrightarrow m=\frac{17}{8}\)

a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2

a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn