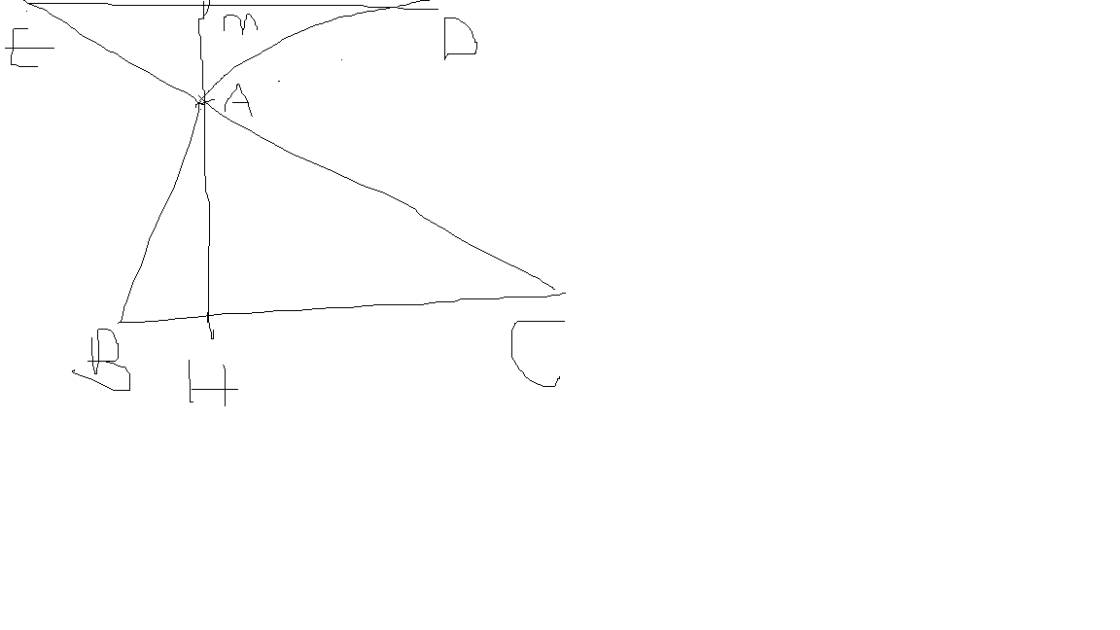
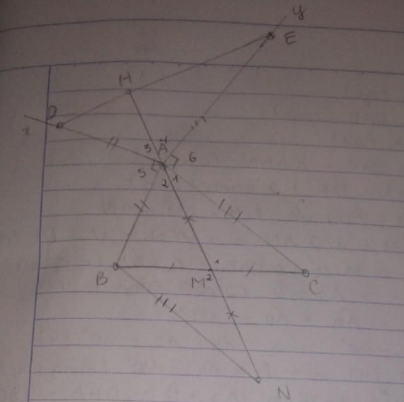
Cho tam giác ABC nhọn . Trên nửa mặt phẳng ko chứa điểm C bờ AB , vẽ tia Ax vuông góc vs AB . Trên tia đó lấy điểm M sao cho AM=AB . Trên nửa mặt phẳng ko chứa điểm B có bờ AC , vẽ tia Ay vuông góc vs AC . Trên tia đó lấy điểm N sao cho AN=AC . Gọi I là trung điểm của MN . Xác định điểm K sao cho I là trung điểm của AK . C/m rằng:
a,AC=MK
b,BC=2AI
c,AI vuông góc vs BC


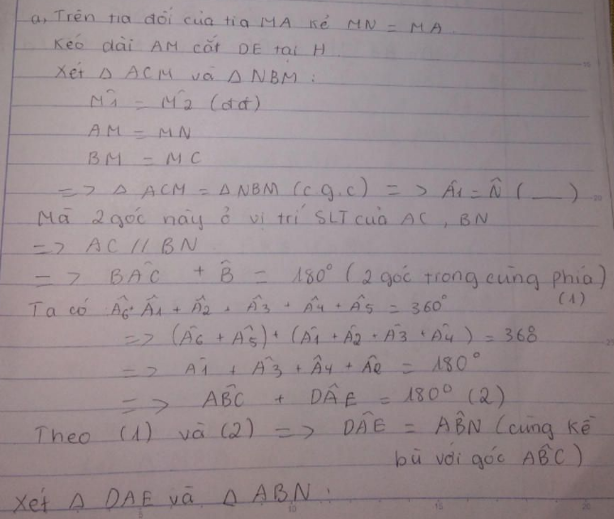
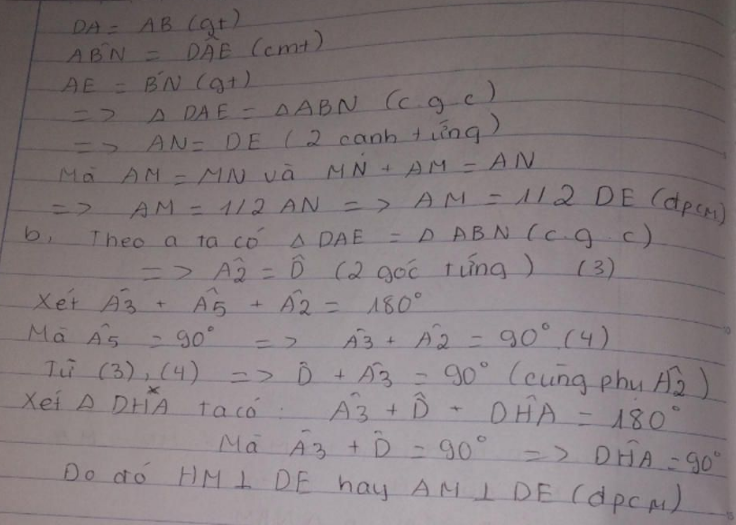
a) Xét ΔKIM và ΔAIN có
KI=AI(I là trung điểm của KA)
\(\widehat{KIM}=\widehat{AIN}\)(hai góc đối đỉnh)
IM=IN(I là trung điểm của MN)
Do đó: ΔKIM=ΔAIN(c-g-c)
nên MK=AN(hai cạnh tương ứng)
mà AN=AC(gt)
nên MK=AC(đpcm)