Cho hai $A(3;5),$ $B(-1;-7)$. Tìm điểm $C$ có hoành độ bằng $1$ sao cho ba điểm $A,$ $B,$ $C$ thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ES
6 tháng 10 2017
Nếu là số dư khác nhau thì a:3 dư 1,b:3 dư 2 hoặc ngược lại.
Nếu vậy thì (a+b) chia hết cho 3 vì số dư là 1+2=3 chia hết cho 3
Đây chỉ là mình nghĩ sao viết vậy thôi nha!
6 tháng 10 2017
Xét các trường hợp:
TH1: a = 3k + 1; b = 3k + 2. ( k là số tự nhiên)
=> a + b = 3k + 1 + 3k + 2 = 6k + 3 = 3.( k + 1 )
Vì 3 chia hết cho 3 => 3.( k + 1 ) chia hết cho 3 hay a + b chia hết cho 3
TH2: a = 3k + 2; b = 3k + 1. ( k là số tự nhiên)
=> a + b = 3k + 2 + 3k + 1 = 6k + 3 = 3.( k + 1 )
Vì 3 chia hết cho 3 => 3.( k + 1 ) chia hết cho 3 hay a + b chia hết cho 3
Vậy ( a + b ) chia hết cho 3
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
CM
6 tháng 4 2017
a → . b → = a → . b → . c o s a → , b → ⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0 .
Đáp án D
CM
24 tháng 5 2017
Ta có a → . b → = a → . b → . c o s a → , b → .
⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0
Chọn D.
PL
0
CM
28 tháng 5 2017
a → = 1 2 + 3 2 = 2 , b → = − 2 3 2 + 6 2 = 48 = 4 3
a → . b → = 1. − 2 3 + 3 .6 = 4 3
cos a → , b → = a → . b → a → b → = 4 3 2.4 3 = 1 2 ⇒ a → , b → = 60
Chọn D
CM
8 tháng 9 2017
Ta có số a không chia hết cho 3 là 4
Số b không chia hết cho 3 là 8
Tổng a + b = 4 + 8 = 12 chia hết cho 3
28 tháng 7 2016
Hiệu hai số là:
17,86 - 9,32 = 8,54
Hiệu số phần bằng nhau là:
3 - 1 = 2 phần
Số bé mới là:
8,54 : 2 = 4,27
Số a là:
9,32 - 4,27 = 5,05
Đáp số : 5,05
28 tháng 7 2016
cho hai số thập phân 17,86 và 9,32 . hãy tìm số a sao cho sau khi bớt a ở hai số ta được hai số có tỉ số là 3 . tìm hai số
Hiệu hai số là:
17,86 - 9,32 = 8,54
Hiệu số phần bằng nhau là:
3 - 1 = 2 phần
Số bé mới là:
8,54 : 2 = 4,27
Số a là:
9,32 - 4,27 = 5,05
Đáp số : 5,05
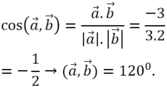
G/s đường thẳng đi qua A và B có công thức \(d:y=ax+b\left(a\ne0\right)\)
Vì \(A\left(3;5\right)\) và \(B\left(-1;-7\right)\) nên ta có: \(\hept{\begin{cases}5=3a+b\\-7=-a+b\end{cases}}\)
Trừ vế với vế đi ta được: \(5-\left(-7\right)=3a+b-\left(-a+b\right)\)
\(\Leftrightarrow4a=12\Rightarrow a=3\Rightarrow b=-4\)
Khi đó đường thẳng d là: \(y=3x-4\)
Vì 3 điểm A,B,C thẳng hàng nên C thuộc đường thẳng d
Mà điểm C có hoành độ là 1 nên thay vào: \(y=3\cdot1-4=-1\)
=> Điểm C có tọa độ (1;-1)
gọi phương trình đường thẳng đi qua AB là y=ax+b
ta có : * 5=3a+b
*-7=-a+b
giải hệ phương trình ta được a=3 và b=-4
vậy phương trình đường thẳng AB là y=3x-4
vì C có hoành độ bằng 1 thay vào phương trình đường thẳng AB ta được
1=3x-4=>x=5/3
vậy c có tọa độ gia điểm (5/3,1) thì A,B,C thẳng hàng