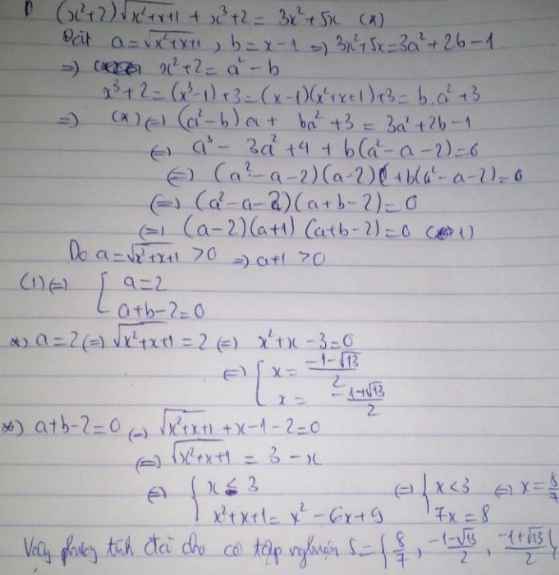Giải PT : 3x^2 + 5x - 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
16 tháng 3 2022
1, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-6\end{matrix}\right.\)
\(A=\left(x_1-2x_2\right)\left(2x_1-x_2\right)\\ =2x_1^2-4x_1x_2-x_1x_2+2x_1^2\\ =2\left(x_1^2+x_2^2\right)-5x_1x_2\\ =2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\\ =2\left(-5\right)^2-4.\left(-6\right)-5.\left(-6\right)\\ =104\)
2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=-3\end{matrix}\right.\)
\(B=x_1^3x_2+x_1x_2^3\\ =x_1x_2\left(x_1^2+x_2^2\right)\\ =\left(-3\right)\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\left(-3\right)\left[5^2-2\left(-3\right)\right]\\ =-93\)
7 tháng 4 2022
1. Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{4}{3}\\x_1.x_2=\dfrac{1}{3}\end{matrix}\right.\)
\(C=\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1^2-x_1+x_2^2-x_2}{x_1x_2-x_1-x_2+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(-\dfrac{4}{3}\right)^2-2.\dfrac{1}{3}-\left(-\dfrac{4}{3}\right)}{\dfrac{1}{3}-\left(-\dfrac{4}{3}\right)+1}=\dfrac{\dfrac{22}{9}}{\dfrac{8}{3}}=\dfrac{11}{12}\)
Y
7 tháng 4 2022
\(1,3x^2+4x+1=0\)
Do pt có 2 nghiệm \(x_1,x_2\) nên theo đ/l Vi-ét ta có :
\(\left\{{}\begin{matrix}S=x_1+x_2=\dfrac{-b}{a}=-\dfrac{4}{3}\\P=x_1x_2=\dfrac{c}{a}=\dfrac{1}{3}\end{matrix}\right.\)
Ta có :
\(C=\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}\)
\(=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_2-1\right)\left(x_1-1\right)}\)
\(=\dfrac{x_1^2-x_1+x_2^2-x_2}{x_1x_2-x_2-x_1+1}\)
\(=\dfrac{\left(x_1^2+x_2^2\right)-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{S^2-2P-S}{P-S+1}\)
\(=\dfrac{\left(-\dfrac{4}{3}\right)^2-2.\dfrac{1}{3}-\left(-\dfrac{4}{3}\right)}{\dfrac{1}{3}-\left(-\dfrac{4}{3}\right)+1}\)
\(=\dfrac{11}{12}\)
Vậy \(C=\dfrac{11}{12}\)
DT
2
HP
5 tháng 2 2022
\(a.-3x^2+15x=0\)
\(\Leftrightarrow3x\left(-x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=0\\-x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
\(b.2x^2-32=0\)
\(\Leftrightarrow2x^2=32\)
\(\Leftrightarrow x^2=16\)
\(\Leftrightarrow\left|x\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
\(c.2x^2-5x+1=0\)
\(a=2;b=-5;c=1\)
\(\Delta=\left(-5\right)^2-4.2.1=17>0\)
Do \(\Delta>0\) nên phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{5+\sqrt{17}}{4}\)
\(x_2=\dfrac{5-\sqrt{17}}{4}\)
5 tháng 2 2022
\(a,-3x^2+15x=0\\ -3x\left(x-5\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
\(b,\\ 2\left(x^2-16\right)=0\\ \Leftrightarrow x^2-16=0\\ \Leftrightarrow\left(x-4\right)\left(x+4\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
\(c,\\ \Delta=5^2-4.2=17\\ \Rightarrow x_1,x_2=\dfrac{\Delta\pm b}{2ac}\\ =\dfrac{5\pm\sqrt{17}}{4}\)
MT
0
MT
2
5 tháng 10 2020
a) 3x2 + 2x - 1 = 0
<=> 3x2 + 3x - x - 1 = 0
<=> 3x( x + 1 ) - ( x + 1 ) = 0
<=> ( x + 1 )( 3x - 1 ) = 0
<=> \(\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}\)
b) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> \(\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\)
c) x2 - 3x + 2 = 0
<=> x2 - x - 2x + 2 = 0
<=> x( x - 1 ) - 2( x - 1 ) = 0
<=> ( x - 1 )( x - 2 ) = 0
<=> \(\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}\)
d) 2x2 - 6x + 1 = 0
<=> 2( x2 - 3x + 9/4 ) - 7/2 = 0
<=> 2( x - 3/2 )2 = 7/2
<=> ( x - 3/2 )2 = 7/4
<=> \(\left(x-\frac{3}{2}\right)=\left(\pm\sqrt{\frac{7}{4}}\right)^2=\left(\pm\frac{\sqrt{7}}{2}\right)^2\)
<=> \(\orbr{\begin{cases}x-\frac{3}{2}=\frac{\sqrt{7}}{2}\\x-\frac{3}{2}=\frac{-\sqrt{7}}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{3+\sqrt{7}}{2}\\x=\frac{3-\sqrt{7}}{2}\end{cases}}\)
NT
3
ND
20 tháng 2 2018
a.
\(2\left(x+5\right)-x^2-5x=0\)
\(\Leftrightarrow2x+10-x^2-5x=0\)
\(\Leftrightarrow-x^2-3x+10=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Leftrightarrow x=2\) hoặc \(x=-5\)
TT
20 tháng 2 2018
a,\(2\left(x+5\right)-x^2-5x=0\)
\(\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\)
\(\Leftrightarrow\left(2-x\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2-x=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
Vậy...
b,\(2x^2+3x-5=0\)
\(\Leftrightarrow2x^2+5x-2x-5=0\)
\(\Leftrightarrow\left(2x^2-2x\right)+\left(5x-5\right)=0\)
\(\Leftrightarrow2x\left(x-1\right)+5\left(x-1\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+5=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)
Vậy...
31 tháng 12 2016
câu trả lời của thu hương rất hay!
Mình làm được khổ nỗi lại chưa biết nghiệm là gì? @ thu hương có thể giải thích cho minh không
hiihhi