K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2023
a)
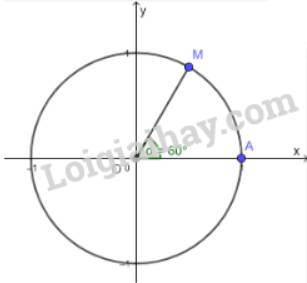
b) \(\cos 60^\circ \) bằng hoành độ của điểm M
\(\sin 60^\circ \) bằng tung độ của điểm M
HQ
Hà Quang Minh
Giáo viên
12 tháng 1
a) Vì \(\Delta DEG \backsim \Delta MNP\) nên \(\widehat D = \widehat M,\,\,\widehat E = \widehat N,\,\,\widehat G = \widehat P\)
\( \Rightarrow \widehat D = \widehat M = 40^\circ \)
\( \to \) Chọn đáp án A.
b) Theo câu a) ta có \(\widehat E = \widehat N = 60^\circ \)
\( \to \) Chọn đáp án C.
c) Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 40^\circ + 60^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 80^\circ \end{array}\)
\( \to \) Chọn đáp án D.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
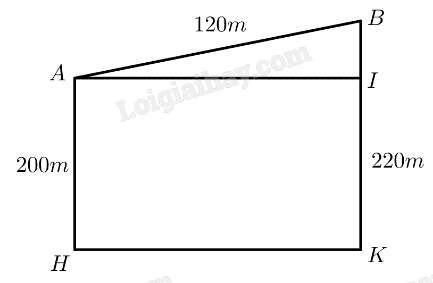
Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Ta có: \(0= 1,8x + 32\)
\(\begin{array}{l} \Rightarrow 1,8x = - 32\\ \Rightarrow x = - 17,(7)\end{array}\)
Vậy \(0 ^\circ F\) tương ứng với \(-17,(7)^0C\)
b) \(T(35) = 1,8 . 35 + 32 = 95 (^\circ F )\)
Vậy nhiệt độ 35\(^\circ \)C tương ứng với 95 \(^\circ \)F
c) Ta có: \(41= 1,8x + 32\)
\(\begin{array}{l} \Rightarrow 1,8x = 41 - 32\\ \Rightarrow 1,8x = 9\\ \Rightarrow x = 5\end{array}\)
Vậy 41\(^\circ \)F tương ứng với 5\(^\circ \)C
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
\( - 4^\circ C\): đọc là “âm bốn độ C” hoặc “trừ bốn độ C”
\( - 10^\circ C\): đọc là “âm mười độ C” hoặc “trừ mười độ C”
\( - 23^\circ C\): đọc là “âm hai mươi ba độ C” hoặc “trừ hai mươi ba độ C”.
21 tháng 8 2023
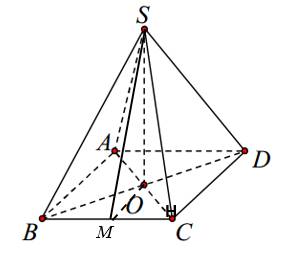
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)
HQ
Hà Quang Minh
Giáo viên
5 tháng 10 2023
1. Độ cao mới của tàu: \( - 0,32 + 0,11 = - \left( {0,32 - 0,11} \right) = -0,21\left( {km} \right)\)
Vậy độ cao mới của tàu là \( - 0,21\left( {km} \right)\) so với mực nước biển.
2. Vì \( - 3,4 > - 49,3\) nên nhiệt độ tại Bắc Cực cao hơn và cao hơn Nam Cực là: \( - 3,4 - \left( { - 49,3} \right) = - 3,4 + 49,3\)\( = 49,3 - 3,4 = 45,9\left( {^\circ C} \right)\)
Vậy nhiệt độ Bắc Cực cao hơn Nam Cực \(45,9\left( {^\circ C} \right)\).
5 tháng 10 2023
Vì 38,83 < 117 nên -117 < -38,38 < 0. Như vậy nhiệt độ đông đặc của rượu thấp nhất, tiếp theo là thủy ngân, sau cùng là nước.
HQ
Hà Quang Minh
Giáo viên
5 tháng 10 2023
Số thập phân âm: \( - 117; - 38,83\)
Số thập phân âm luôn nhỏ hơn 0 nên \( - 117 < 0; - 38,83 < 0\)
Vì \(117 > 38,83\) nên \( - 117 < - 38,83\)
Dó đó \( - 117 < - 38,83 < 0\)
Vậy nhiệt độ đông đặc của ba chất này theo thứ tự từ nhỏ đến lớn là: rượu, thủy ngân, nước.
HQ
Hà Quang Minh
Giáo viên
5 tháng 10 2023
a) Vì 51,2 > 38,83 nên -51,2 < -38,83 nên ở nhiệt độ \( - 51,2^\circ C\) thì thủy ngân ở thể rắn.
b) Nhiệt độ của tủ phải tăng thêm số độ để lượng thủy ngân bắt đầu bay hơi là:
\(356,73 - (-51,2)= 407,93 ^\circ C\)