Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(2x+xy+y=3\Leftrightarrow2x+xy+y+2=5\)
\(\Leftrightarrow\left(x+1\right)\left(y+2\right)=5=5.1=-5.\left(-1\right)\)
Đến đây giải nghiệm nguyên như bình thường!
b/
\(\frac{1}{x}+\frac{1}{y}=2\Leftrightarrow\frac{x+y}{xy}=2\Leftrightarrow x+y=2xy\)
\(\Leftrightarrow4xy-2x-2y=0\Leftrightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=-1.\left(-1\right)\)
Đến đây giải nghiệm nguyên như bình thường!

a) (x+1)(3-y)=5
=> x+1 ; 3-y thuộc Ư(5)={-1,-5,1,5}
Ta có bảng :
| x+1 | -1 | -5 | 1 | 5 |
| 3-y | -5 | -1 | 5 | 1 |
| x | -2 | -6 | 0 | 4 |
| y | 8 | 4 | -2 | 2 |
Vậy ta có các cặp x,y thõa mãn là : (-2,8);(-6,4);(0,-2);(4,2)
b) (2x+1)(y-2)=10
=> 2x+1 ; y-2 thuộc Ư(10)={-1,-2,-5,-10,1,2,5,10}
Ta có bảng :
| 2x+1 | -1 | -2 | -5 | -10 | 1 | 2 | 5 | 10 |
| y-2 | -10 | -5 | -2 | -1 | 10 | 5 | 2 | 1 |
| x | -1 | -3/2 (loại) | -3 | -11/2 (loại) | 0 | 1/2 (loại) | 2 | 9/2 (loại) |
| y | -8 | -3 | 0 | 1 | 12 | 7 | 4 | 3 |
Vậy ta có các cặp x,y thõa mãn là : (-1,-8);(-3,0);(0,12);(2,4)

\(a,x-5⋮x+2\)
\(\Rightarrow x+2-7⋮x+2\)
\(\Rightarrow x+2\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
x + 2 = 1=> x = -1
x + 2 = -1 => x = -3
.... tương tự nhé ~
\(2x+3⋮x-5\)
\(\Rightarrow2x-10+7⋮x-5\)
\(\Rightarrow2\left(x-5\right)+7⋮x-5\)
\(\Rightarrow x-5\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
x - 5 = 1 => x = 6
....

a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
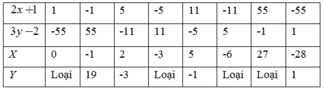
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
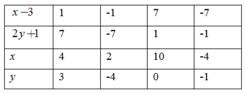
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.

a,Vì x,y thuộc Z nên \(\hept{\begin{cases}x+3\\y+1\end{cases}\in Z}\)
\(\Rightarrow\left(x+3\right);\left(y+1\right)\inƯ\left(3\right)\)
\(\Rightarrow\left(x+3\right);\left(y+1\right)\in\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\orbr{\begin{cases}x+3=1\Rightarrow x=-2\\y+1=3\Rightarrow y=2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x+3=-1\Rightarrow x=-4\\y+1=-3\Rightarrow y=-4\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x+3=3\Rightarrow x=0\\y+1=1\Rightarrow y=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x+3=-3\Rightarrow x=-6\\y+1=-1\Rightarrow x=-2\end{cases}}\)
a) Ta có: (x-2)(y+1)=-1
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2=1\\y+1=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=-1\\y+1=1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\end{matrix}\right.\)
Vậy: (x,y)={(3;-2);(1;0)}
b) Ta có: \(\left(2x+1\right)\left(y-2\right)=3\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x+1=1\\y-2=3\end{matrix}\right.\\\left\{{}\begin{matrix}2x+1=3\\y-2=1\end{matrix}\right.\\\left\{{}\begin{matrix}2x+1=-1\\y-2=-3\end{matrix}\right.\\\left\{{}\begin{matrix}2x+1=-3\\y-2=-1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x=0\\y=5\end{matrix}\right.\\\left\{{}\begin{matrix}2x=2\\y=3\end{matrix}\right.\\\left\{{}\begin{matrix}2x=-2\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}2x=-4\\y=1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=5\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\\\left\{{}\begin{matrix}x=-1\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\end{matrix}\right.\)
Vậy: (x,y)={(0;5);(1;3);(-1;-1);(-2;1)}