K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
Độ dài đáy của hình bình hành đó là:
`12 \times 2 = 24 (cm)`
S của hình bình hành đó là:
`12 \times 24 =288 (cm^2)`
Đáp số: `288 cm^2.`
8 tháng 8 2023
Giải :
Độ dài cạnh đáy là :
12 x 3 = 26 ( m )
Diện tích hình bình hành là :
12 x 36 = 432 ( m2 )
Đ/s :..............
31 tháng 3 2022
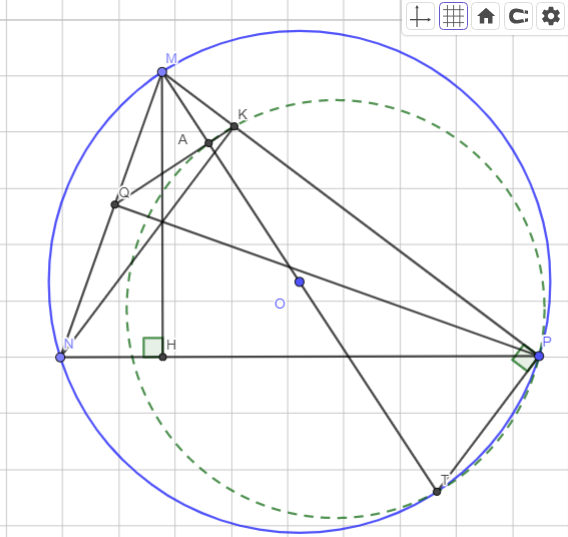
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
29 tháng 3 2022
Dạ bài anh có nhầm lẫn gì kh ạ chứ khúc đầu e thấy hơi sai sai 😅😅
TP
19 tháng 12 2021
Tham khảo
| STT | Tên loài giáp xác | Loài địa phương đã gặp | Nơi sống | Có nhiều hay ít |
| 1 | Mọt ẩm | Mọt ẩm | Ẩm ướt | Ít |
| 2 | Con sun | Không | Ở biển | Ít |
| 3 | Rận nước | Rận nước | Ở nước | Ít |
| 4 | Chân kiếm | Không có | Ở nước | Ít |
| 5 | Cua đồng | Cua đồng | Hang hốc | Nhiều |
| 6 | Cua nhện | Không | Ở biển | Ít |
| 7 | Tôm ở nhờ | Không | Ở biển | Ít |
23 tháng 10 2023
\(tana=\sqrt{3}\)
=>\(\dfrac{sina}{cosa}=\sqrt{3}\)
=>\(sina=\sqrt{3}\cdot cosa\)
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+3=4\)
=>\(cos^2a=\dfrac{1}{4}\)
=>\(cosa=\dfrac{1}{2}\)
=>\(sina=\dfrac{\sqrt{3}}{2}\)
\(A=\dfrac{sin^2a-cos^2a}{sina\cdot cosa}\)
\(=\dfrac{\dfrac{3}{4}-\dfrac{1}{4}}{\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}}=\dfrac{2}{4}:\dfrac{\sqrt{3}}{4}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\)
22 tháng 7 2023
Độ dài của chiều cao là:
12:2=6(cm)
=>Diện tích hình bình hành đó là:
12x6=72(cm2)
Đáp số:72 cm2
DT
Đỗ Thanh Hải
CTVVIP
21 tháng 3 2021
1 does => did
2 build => be built
3 hold => held
4 will => would
5 rice-exported => rice-exporting
6 invite => inviting
7 finish products => finished products
8 have to=> had to
9 was appeared => appeared
10 were perform => were performed
11 making => to make
12 to participate => participate
13 told that => said that
14 design => designed
15 ice-skate => ice - skating
7 tháng 7 2018
Đề bài mình nghĩ là đúng, còn về cách làm thì bạn theo công thức " số lớn nhất thỏa mãn trừ đi số nhỏ nhất thỏa mãn, rồi chia cho khoảng cách giữa các số rồi cộng 1"
BN
3
NN
1
Câu 1:
a) \(3x\left(x-2\right)+5\left(x-2\right)=\left(3x+5\right)\left(x-2\right)\).
b) \(x^2-2x-9y^2-6y=\left(x^2-9y\right)-2\left(x+3y\right)=\left(x-3y\right)\left(x+3y\right)-2\left(x+3y\right)=\left(x-3y-2\right)\left(x+3y\right)\)c) \(x^4+x^3+2x^2+x+1=\left(x^4+x^3+x^2\right)+\left(x^2+x+1\right)=\left(x^2+1\right)\left(x^2+x+1\right)\).
Câu 1 :
a, \(3x\left(x-2\right)+5\left(x-2\right)=\left(3x+5\right)\left(x-2\right)\)
b, \(x^2-2x-9y^2-6y=\left(x^2-9y^2\right)+\left(-2x-6y\right)\)
\(=\left(x-3y\right)\left(x+3y\right)-2\left(x+3y\right)=\left(x-3y-2\right)\left(x+3y\right)\)
c, \(x^4+x^3+2x^2+x+1=\left(x^4+2x^2+1\right)+\left(x^3+x\right)\)
\(=\left(x^2+1\right)+x\left(x^2+1\right)=\left(x+1\right)\left(x^2+1\right)\)
nhẹ ngàng tình cảm :>>