Tìm x biết: (x-1)^2019+(x-1)^2020=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2019
a) (x - 1)3 - 1 = 0
<=> (x - 1)3 = 0 + 1
<=> (x - 1)3 = 1
<=> (x - 1)3 = 13
<=> x - 1 = 1
<=> x = 1 + 1
<=> x = 2
=> x = 2
b) (x - 4)2019 = 1
<=> (x - 4)2019 = 12019
<=> x - 4 = 1
<=> x = 1 + 4
<=> x = 5
=> x = 5
c) (x - 2019)2020 = 0
<=> (x - 2019)2020 = 02020
<=> x - 2019 = 0
<=> x = 0 + 2019
<=> x = 2019
=> x = 2019
d) (x - 1)2 = (x - 1)3
<=> x2 - 2x + 1 = x3 - 2x2 + x - x2 + 2x - 1
<=> x2 - 2x + 1 = x3 - 3x2 + 3 - 1
<=> x2 - 2x + 1 - x3 + 3x2 - 3 + 1 = 0
<=> 4x2 - 5x + 2 - x3 = 0
<=> (-x2 + 3x - 2)(x - 1) = 0
<=> (x2 - 3x + 2)(x - 1) = 0
<=> (x - 2)(x - 1)(x - 1) = 0
<=> x - 2 = 0 hoặc x - 1 = 0
x = 0 + 2 x = 0 + 1
x = 2 x = 1
=> x = 1 hoặc x = 2
19 tháng 12 2019
Cho a,b,c khác 0 t/m:
1/a+1/b+1/c=1/2018 và a+b+c=2018
cmr" 1/a^2019+1/b^2019+1/c^2019=1/(a^2019+b^2019+c^2019)
Ta có :
gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3
Đến đây là dạng của phương trình ước số bạn chỉ cần xét ước của 33 là sẽ tìm được nghiệm nguyên của PT
TM
7
9 tháng 1 2018
a ) 4 . ( x2 + 1 ) = 0
x2 + 1 = 0 : 4
x2 + 1 = 0
x2 = 0 - 1
x2 = - 1
x2 = - 12 => x = - 1
Vậy x = - 1
BL
0
BL
1
4
K
26 tháng 7 2019
Ta có: |x - 2019| ≥ 0 => |x - 2019|2019 ≥ 0
|x - 2020| ≥ 0 => |x - 2020|2020 ≥ 0
+) TH1: \(\hept{\begin{cases}\left|x-2019\right|^{2019}=0\\\left|x-2020\right|^{2020}=1\end{cases}\Rightarrow}\hept{\begin{cases}\left|x-2019\right|=0\\\left|x-2020\right|=1\end{cases}}\Rightarrow\hept{\begin{cases}x-2019=0\\\left|x-2020\right|=1\end{cases}\Rightarrow}\hept{\begin{cases}x=2019\\\left|x-2020\right|=1\end{cases}}\)
Giải: |x - 2020| = 1
TH1: x - 2020 = 1 => x = 2021
TH2: x - 2020 = -1 => x = 2019
Vì 2021 ≠ 2019
=> x = 2019
+) TH2: \(\hept{\begin{cases}\left|x-2019\right|^{2019}=1\\\left|x-2020\right|^{2020}=0\end{cases}\Rightarrow}\hept{\begin{cases}\left|x-2019\right|=1\\\left|x-2020\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}\left|x-2019\right|=1\\x-2020=0\end{cases}\Rightarrow}\hept{\begin{cases}\left|x-2019\right|=1\\x=2020\end{cases}}\)
Giải |x - 2019| = 1
Th1: x - 2019 = 1 => x = 2020
Th2: x - 2019 = -1 => x = 2018
Vì 2018 ≠ 2020
=> x = 2020
Vậy x \(\in\){ 2020; 2019 }
P/s: Ko chắc :)
O
0
WT
2
TT
16 tháng 2 2020
\(\left(x+20\right)^{2020}+\left|y+4\right|^{2019}=0\)
Ta thấy : \(\hept{\begin{cases}\left(x+20\right)^{2020}\ge0\forall x\\\left|y+4\right|^{2019}\ge0\forall y\end{cases}}\)
\(\Rightarrow\left(x+20\right)^{2020}+\left|y+4\right|^{2019}\ge0\forall x,y\)
Do đó, dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x+20\right)^{2020}=0\\\left|y+4\right|^{2019}=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=-20\\y=-4\end{cases}}\)
Vậy : \(\left(x,y\right)=\left(-20,-4\right)\)
16 tháng 2 2020
( x + 20 )2020 + | y + 4 |2019 = 0
Vì ( x + 20 )2020 \(\ge\)0
| y + 4 |2019 \(\ge\) 0
=> ( x + 20 )2020 + | y + 4 |2019 \(\ge\)0
Dấu " = " xảy ra khi
\(\hept{\begin{cases}x+20=0\\y+4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-20\\y=-4\end{cases}}}\)
Vậy ................................
DH
1
30 tháng 3 2022
\(\Leftrightarrow\dfrac{x-2}{2020}-1+\dfrac{x-3}{2019}-1=\dfrac{x-2019}{3}-1+\dfrac{x-2020}{2}-1\)
=>x-2022=0
hay x=2022
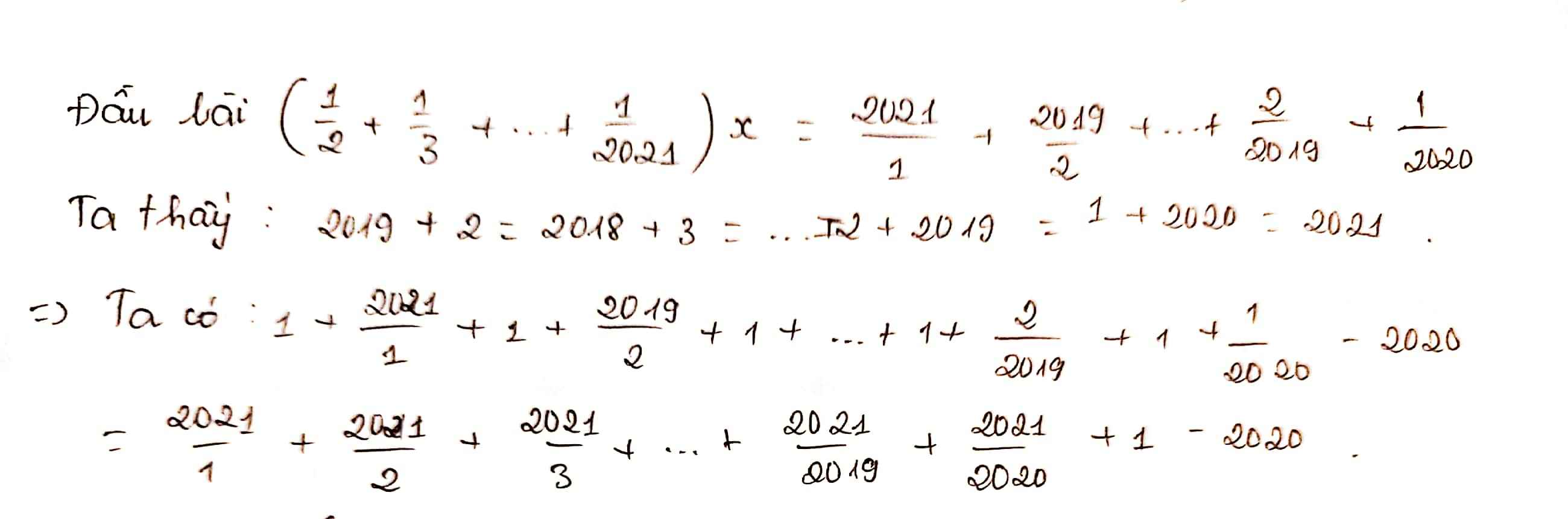
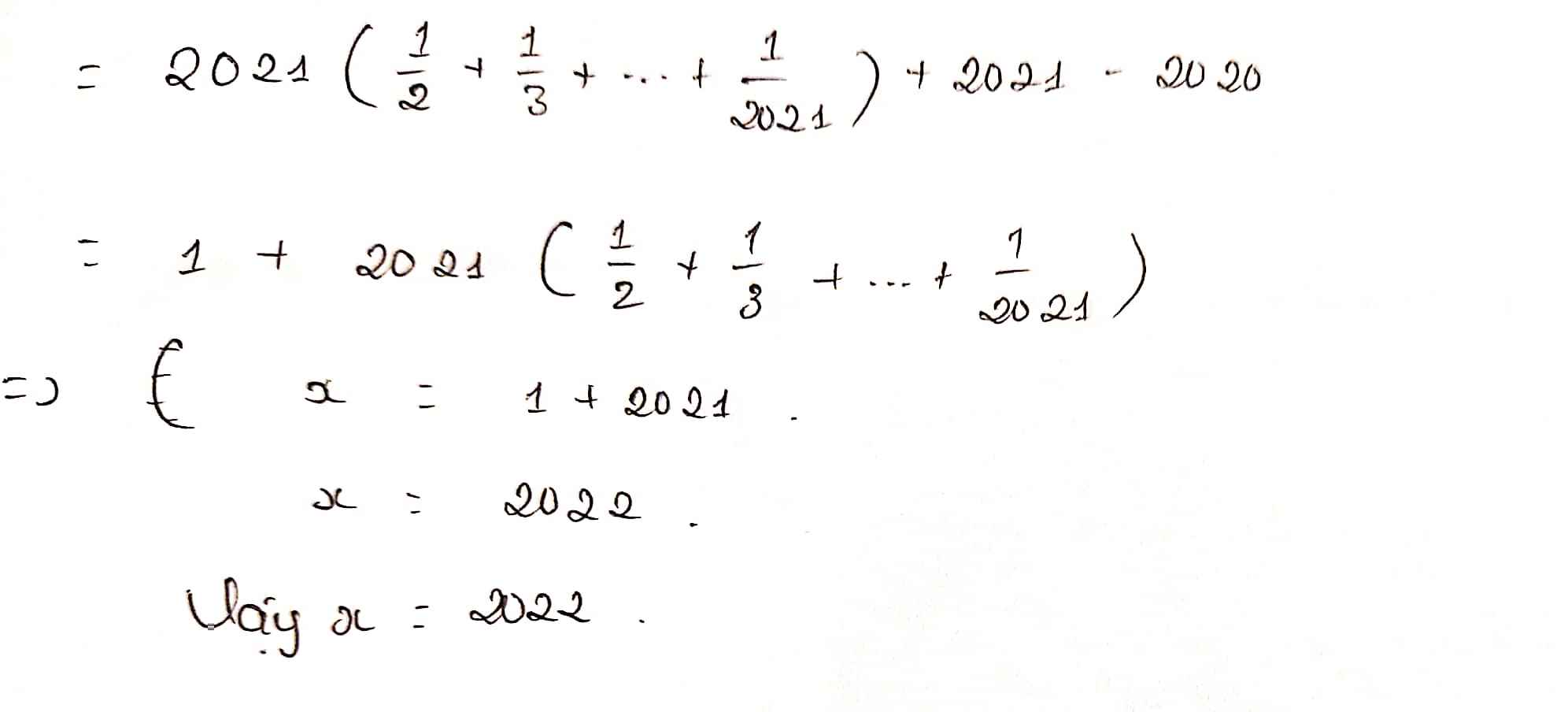
Cách 1 : \(\left(x-1\right)^{2019}+\left(x-1\right)^{2020}=0\)
Vì \(\left(x-1\right)^{2019}\ge0\forall x;\left(x-1\right)^{2020}\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^{2019}+\left(x-1\right)^{2020}\ge0\forall x\)
Dấu ''='' xảy ra <=> x = 1
Cách 2 : \(\left(x-1\right)^{2019}+\left(x-1\right)^{2020}=0\)
\(\Leftrightarrow\left(x-1\right)^{2019}\left[1+\left(x-1\right)\right]=0\)
\(\Leftrightarrow x\left(x-1\right)^{2019}=0\Leftrightarrow x=0;1\)