Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2-2\left(m-1\right)x-2m=0\)
\(\text{Δ}=\left(-2m+2\right)^2-4\cdot1\cdot\left(-2m\right)\)
\(=4m^2-8m+4+8m=4m^2+4>=4>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt

Nếu phương trình là \(\left(2m^2-5m+2\right)\left(x-1\right)^{2021}\left(x^{2020}-2\right)+2x^2-3=0\) thì còn có cơ hội giải quyết
Chứ đề đúng thế này thì e rằng không có cơ hội nào cả.

\(\Leftrightarrow3\left|x-1\right|+6-3m=\left|x-1\right|+m-5\)
\(\Leftrightarrow2\left|x-1\right|=4m-11\)
Do \(2\left|x-1\right|\ge0\) với mọi x nên pt có nghiệm khi:
\(4m-11\ge0\Rightarrow m\ge\dfrac{11}{4}\)

a, \(\left(x+m\right)m+x>3x+4\)
\(\Leftrightarrow mx+m^2+x>3x+4\)
\(\Leftrightarrow\left(m-2\right)x+m^2-4>0\left(1\right)\)
Nếu \(m=0,\) bất phương trình vô nghiệm
Nếu \(m>0\)
\(\left(1\right)\Leftrightarrow x>-m-2\)
\(\Rightarrow x\in\left(-m-2;+\infty\right)\)
\(\Rightarrow m>0\) thỏa mãn yêu cầu bài toán
Nếu \(m< 0\)
\(\left(1\right)\Leftrightarrow x< -m-2\)
\(\Rightarrow\) Không thỏa mãn
Vậy \(m>0\)
b, \(m\left(x-m\right)\ge x-1\)
\(\Leftrightarrow mx-m^2\ge x-1\)
\(\Leftrightarrow\left(m-1\right)x\ge m^2-1\left(1\right)\)
Nếu \(m=1,\) bất phương trình thỏa mãn
Nếu \(m>1\)
\(\left(1\right)\Leftrightarrow x\ge m+1\)
\(\Rightarrow m>1\) không thỏa mãn yêu cầu
Nếu \(m< 1\)
\(\left(1\right)\Leftrightarrow x\le m+1\)
\(\Rightarrow m< 1\) thỏa mãn yêu cầu bài toán
Vậy \(m< 1\)

ĐKXĐ: \(-1\le x\le1\)
Đặt \(\sqrt{1-x^2}=t\Rightarrow0\le t\le1\)
\(\Rightarrow x^2=1-t^2\)
Phương trình trở thành: \(1-t^2+t=m\Leftrightarrow-t^2+t+1=m\)
Xét hàm \(f\left(t\right)=-t^2+t+1\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=1\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{5}{4}\) ; \(f\left(1\right)=1\)
\(\Rightarrow1\le f\left(t\right)\le\dfrac{5}{4}\)
\(\Rightarrow\) Pt đã cho có nghiệm khi và chỉ khi \(1\le m\le\dfrac{5}{4}\Rightarrow S=\dfrac{9}{4}\)

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)


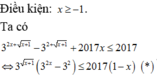

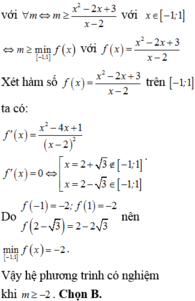
Help me
\(\Leftrightarrow\left(m^2+3\right)x-m^2-3-m=\left(3-2m\right)x-5\)
\(\Leftrightarrow\left(m^2+3-3+2m\right)x=m^2+m+3-5\)
\(\Leftrightarrow\left(m^2+2m\right)x=m^2+m-2\)
Pt có tập nghiệm R khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2+2m=0\\m^2+m-2=0\end{matrix}\right.\) \(\Leftrightarrow m=-2\)