một nhóm có 13 nam, 9 nữ
Chọn 11 bạn trong nhóm. Tính xác suất để 11 bạn được chọn có cả nam và nữ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 4 2023
a. \(C^1_7=7\left(cách\right)\)
b. \(C^1_3=3\left(cách\right)\)
c. Số cách không ra bạn nữ là chỉ chọn nam, vậy số cách chọn ít nhất 1 nữ là: \(7-3=4\left(cách\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2022
Không gian mẫu: \(C_5^3=10\)
Chọn 3 bạn có ít nhất 2 nữ: ta có 2 trường hợp thuận lợi là 2 nữ 1 nam và 3 bạn đều nữ
\(\Rightarrow C_2^1.C_3^2+C_3^3=7\) cách
Xác suất: \(P=\dfrac{7}{10}\)
CM
19 tháng 2 2018
Gọi A là biến cố: “5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ “
- Số phần tử của không gian mẫu: Ω = C 15 5 .
-Số cách chọn 5 bạn trong đó có 4 nam, 1 nữ là: C 8 4 . C 7 1 .
- Số cách chọn 5 bạn trong đó có 3 nam, 2 nữ là: C 8 3 . C 7 2 .
Số cách chọn 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
n A = C 8 4 . C 7 1 + C 8 3 . C 7 2 = 1666
Xác suất để 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
P A = n A Ω = 1666 C 15 5 = 238 429 .
Chọn đáp án B.
6 tháng 1 2023
\(n\left(\Omega\right)=C^2_8\)
\(n\left(A\right)=C^2_5\)
=>P(A)=5/14
CM
21 tháng 10 2019
Chọn A
Lời giải. Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * )
Suy ra số học sinh nữ trong nhóm B là
25 - 9 - x - y = 16 - x - y
Khi đó, nhóm A có: 9 nam, x nữ và nhóm B có
y nam, 16 - x - y nữ
Xác suất để chọn được hai học sinh nam là
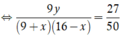
Mặt khác x + y < 16
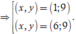
Vậy xác suất để chọn đươc hai học sinh nữ là
C 1 1 . C 6 1 C 10 1 . C 15 1 = 0 , 04
CM
2 tháng 1 2020
Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
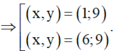
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.
CM
25 tháng 5 2018
Chọn B.
Số phần tử của không gian mẫu:
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: 
.
CM
12 tháng 3 2019
Đáp án B
Gọi x,y lần lượt là số học sinh nữ ở nhóm I và nhóm II. Khi đó số học sinh nam ở nhóm II là 25 − 9 + x − y = 16 − x − y . Điều kiện để mỗi nhóm đều có học sinh nam và nữ là x ≥ 1, y ≥ 1,16 − x − y ≥ 1 ; x , y ∈ ℕ .
Xác suất để chọn ra được hai học sinh nam bằng C 9 1 C 16 − x − y 1 C 9 + x 1 C 16 − x 1 = 0,54
⇔ 9 16 − x − y 9 + x 16 − x = 0,54 ⇔ 144 − 9 x − 9 y 144 + 7 x − x 2 = 0,54 ⇔ y = 184 25 − 71 50 x + 3 50 x 2
Ta có hệ điều kiện sau x ≥ 1 184 25 − 71 50 x + 3 50 x 2 ≥ 1 16 − x − 184 25 − 71 50 x + 3 50 x 2 ≥ 1 x ∈ ℕ
⇔ x ≥ 1 3 50 x 2 − 71 50 x + 159 25 ≥ 0 − 3 50 x 2 + 21 50 x + 191 25 ≥ 0 x ∈ ℕ ⇔ x ≥ 1 x ≥ 53 3 x ≤ 6 21 − 5 201 6 ≤ x ≤ 21 + 5 201 6 x ∈ ℕ ⇔ 1 ≤ x ≤ 6 x ∈ ℕ
Ta có bảng các giá trị của :
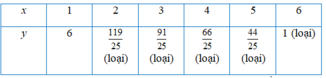
Vậy ta tìm được hai cặp nghiệm nguyên x ; y thỏa mãn điều kiện là 1 ; 6 và 6 ; 1 .
Xác suất để chọn ra hai học sinh nữ là C x 1 C y 1 C 9 + x 1 C 16 − x 1 = x y 9 + x 16 − x .
Nếu x ; y ∈ 1 ; 6 , 6 ; 1 thì xác suất này bằng 1 25 = 0,04 .
Không gian mẫu: \(C_{22}^{11}\)
Số cách chọn 11 bạn chỉ có nam hoặc nữ: \(C_{13}^{11}\)
Xác suất: \(P=\dfrac{C_{22}^{11}-C_{13}^{11}}{C_{22}^{11}}=...\)