Gọi A là tập hợp các số tự nhiên có 3 chữ số, các chữ số phân biệt được lập từ các chữ số 0,1,2,3,4,5,6. Chọn một số từ tập hợp A.
Tính xác suất để:
a) số được chọn là số chẵn
b) số được chọn chia hết cho 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập S có 9 4 phần tử. Ta có
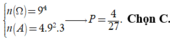
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
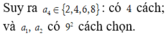
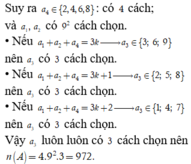

Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)

Đáp án A
Gọi số cần tìm có dạng a b c d ¯ vì a b c d ¯ chia hết cho 6 ⇒ d = { 2 ; 4 ; 6 ; 8 } a + b + c + d : 3 .
Khi đó, chọn d có 4 cách chọn; b và c đều có 9 cách chọn (từ 1 → 9 )
Nếu b + c + d:3 thì a = {3;6;9} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 1 thì a = {2;5;8} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 2 thì a = {1;4;7} ⇒ có 3 cách chọn a
Suy ra a chỉ có 3 cách chọn ⇒ có 4.9.9.3 = 972 số chia hết cho 6
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .

Đáp án A.
Gọi số cần tìm có dạng a b c d vì chia hết cho 6
⇒ d = { 2 , 4 , 6 , 8 } a + b + c + d : 3
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1 → 9).
+) Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .
Gọi số đó là \(\overline{abc}\)
Không gian mẫu: \(6.6.5=180\)
a. TH1: \(c=0\Rightarrow ab\) có \(A_6^2\) cách
TH2: \(c\ne0\Rightarrow c\) có 3 cách chọn, ab có \(5.5=25\) cách
Xác suất: \(P=\dfrac{3.25+A_6^2}{180}=\)
b. Tổng 3 chữ số chia hết cho 3 khi 3 số đồng dư khi chia 3 hoặc 3 số đôi một khác số dư khi chia 3.
- 3 số đồng dư khi chia cho 3: \(3!-2!=4\) số
- 3 số chia 3 có 3 số dư khác nhau:
+ Không có mặt số 0: \(C_2^1C_2^1C_2^1.3!=48\)
+ Có mặt số 0: \(C_2^1C_2^1C_2^1\left(3!-2!\right)=32\)
Xác suất: \(P=\dfrac{4+48+32}{180}=...\)
Cho em hỏi ở TH1 của câu a, khi c = 0, ab có sắp thứ tự nên phải là \(A^2_6\) cách chứ đúng không ạ...