tính a= x^3-y^3 và x+y=3 , x^2+y^2=149
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
1
22 tháng 12 2016
(x-y)^2=9
x^2-2xy+y^2=9
-2xy=9-149
xy=70
x^2+y^2=149
x^2+2xy+y^2=149+2.70
(x+y)^2=289
x+y=17 hoặc x+y=-17
giải theo kiểu tổng hiệu ra kết quả x=10 và y=7 hoặc x=-7 và y=-10
FF
17 tháng 8 2016
1) Cho x+y=2 và x^2+y^2=10. Tính x^3+y^3. Giải
(x+y)^2=x^2+y^2+2xy => xy= -3
x^3+y^3=(x+y)^3-3xy(x+y) = 26
2) Ta có: x^3+y^3 = (x+y)(x^2-xy+y^2) (1)
(x+y)^2=a^2
=> x^2 +2xy +y^2=a^2
=> b+2xy=a^2
=> xy=\(\frac{a^2-b}{2}\)
Thay (1) vào đó ta có:
x^3+y^3= (x+y)(x^2-xy+y^2) = a(b-\(\frac{a^2-b}{2}\)) = \(a\left(\frac{2b-a^2+b}{2}\right)=a.\frac{3b-a^2}{2}\)
17 tháng 8 2016
\(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=2\left(10-xy\right)\)
Ta có: \(x^2+y^2=\left(x+y\right)^2-2xy=2^2-2xy=4-2xy=10\Rightarrow2xy=-6\Rightarrow xy=-3\)
Vậy: \(x^3+y^3=2\left(10+3\right)=2.13=26\)
NH
13 tháng 7 2019
a, x + y = 3 => (x + y)2 = 9 <=> x2 + 2xy + y2 = 9 <=> 5 + 2xy = 9 <=> 2xy = 4 <=> xy = 2
Ta có: x3 + y3 = (x + y)(x2 - xy + y2) = 3 . (5 - 2) = 3 . 3 = 9
b, x - y = 5 => (x - y)2 = 25 <=> x2 - 2xy + y2 = 25 <=> 15 - 2xy = 25 <=> -2xy = 10 <=> xy = -5
Ta có: x3 - y3 = (x - y)(x2 + xy + y2) = 5 . (15 - 5) = 5 . 10 = 50
DD
Đoàn Đức Hà
Giáo viên
27 tháng 6 2021
a) \(\left(x+y\right)^2=x^2+y^2+2xy\Rightarrow4=10+2xy\Leftrightarrow xy=-3\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=2^3+3.3.2=26\)
b) \(\left(x-y\right)^2=x^2+y^2-2xy\Rightarrow m^2=n-2xy\Leftrightarrow xy=\frac{n-m^2}{2}\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=m^3+3.m.\frac{n-m^2}{2}=\frac{3mn}{2}-\frac{m^3}{2}\)
8 tháng 8 2017
(x+y)^2 =a^2
x^2 +2xy +y^2 =a^2
x^2+y^2 =a^2-2xy =a^2 -2b
x^3 +y^3 = (x+y)(x^2 -xy +y^2)
=a(a^2-2b-b)
=a(a^2-3b)
=a^3- 3ab
(x^2 +y^2)^2=(a^2-2b)^2 ( cái này tính cho x^4 + y^4)
tương tự như câu đầu tiên
x^5+ y^5 (cái đó mình không biết)
CG
1
NM
Nguyễn Minh Quang
Giáo viên
12 tháng 8 2021
a. ta có : \(x^2+y^2=\left(x+y\right)^2-2xy=1^2-2\times\left(-6\right)=13\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=1^3-3\times\left(-6\right)\times1=19\)
\(x^5+y^5=\left(x+y\right)\left[x^4-x^3y+x^2y^2-xy^3+y^4\right]\)
\(=\left(x+y\right)\left[\left(x^2+y^2\right)^2-x^2y^2-xy\left(x^2+y^2\right)\right]=1.\left(13^2-\left(-6\right)^2-\left(-6\right).13\right)=211\)
b.\(x^2+y^2=\left(x-y\right)^2+2xy=1+2\times6=13\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=1^3+6.3.1=19\)
\(x^5-y^5=\left(x-y\right)\left[\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\right]\)
\(=\left(x-y\right)\left[\left(x^2+y^2\right)^2-x^2y^2+xy\left(x^2+y^2\right)\right]=1.\left(13^2-6^2+6.13\right)=211\)
22 tháng 7 2023
`a, (x-y)^2 = (x+y)^2 - 4xy = 12^2 - 35 . 4 = 144 - 140 = 4`.
`b, (x+y)^2 = (x-y)^2 + 4xy = 8^2 + 20.4 = 64 + 80 = 144`
`c, x^3 + y^3 = (x+y)^3 - 3xy(x+y) = 5^3 - 3 . 6 . 5 = 125 - 90 = 35`
`d, x^3 - y^3 = (x-y)^3 - 3xy(x-y) = 3^3 - 3 .40 . 3 = 27 - 360 = -333`.
LV
2
17 tháng 8 2021
a: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=3^3-3\cdot3\cdot\left(-2\right)\)
\(=27+18=45\)
b: \(\left(x^3+y^3\right)^2=45^2=2025\)
24 tháng 9 2020
Bài 1.
A = x2 + 2xy + y2 = ( x + y )2 = ( -1 )2 = 1
B = x2 + y2 = ( x2 + 2xy + y2 ) - 2xy = ( x + y )2 - 2xy = (-1)2 - 2.(-12) = 1 + 24 = 25
C = x3 + 3xy( x + y ) + y3 = ( x3 + y3 ) + 3xy( x + y ) = ( x + y )( x2 - xy + y2 ) + 3xy( x + y )
= -1( 25 + 12 ) + 3.(-12).(-1)
= -37 + 36
= -1
D = x3 + y3 = ( x3 + 3x2y + 3xy2 + y3 ) - 3x2y - 3xy2 = ( x + y )3 - 3xy( x + y ) = (-1)3 - 3.(-12).(-1) = -1 - 36 = -37
24 tháng 9 2020
Bài 2.
M = 3( x2 + y2 ) - 2( x3 + y3 )
= 3( x2 + y2 ) - 2( x + y )( x2 - xy + y2 )
= 3( x2 + y2 ) - 2( x2 - xy + y2 )
= 3x2 + 3y2 - 2x2 + 2xy - 2y2
= x2 + 2xy + y2
= ( x + y )2 = 12 = 1
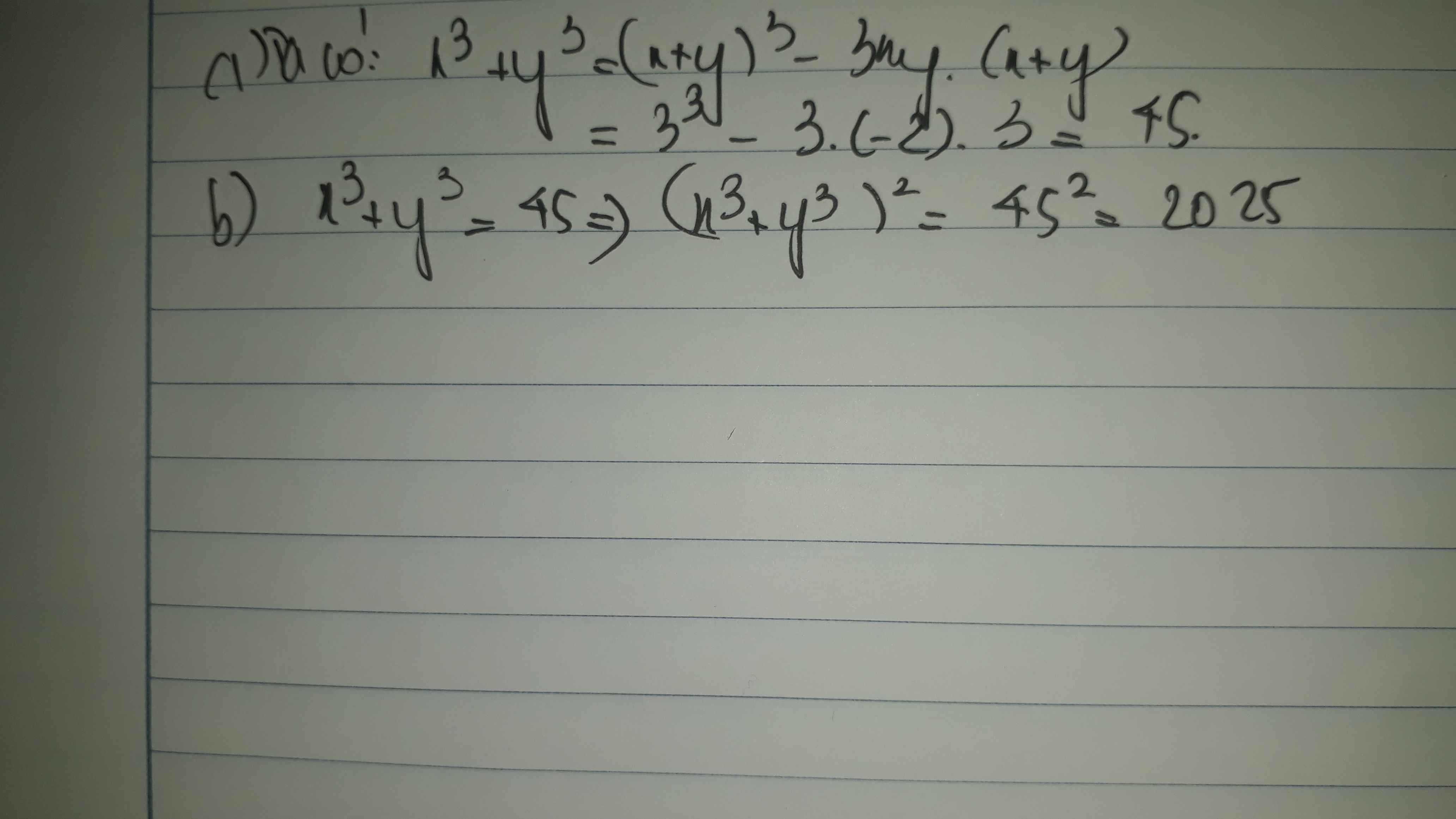
Ta có : A = x3 - y3
= (x - y)(x2 + xy + y2)
= (x - y)3 + 3xy(x - y)
Vì x + y = 3
=> (x + y)2 = 9
=> x2 + y2 + 2xy = 9
=> 149 + 2xy = 9
=> 2xy = -140
=> xy = -70
Khi đó (x - y)2 = x2 + y2 - 2xy = 149 + 2.70 = 289
=> (x - y)2 = 172
=> x - y = \(\pm\)17
Khi x - y = 17
=> A = (x - y)3 + 3xy(x - y)
= 173 + 3.(-70).17 = 1343
Khi x - y = -17
=> A = (x - y)3 + 3xy(x - y)
= (-17)3 + 3.(-70).(-17)
= -1343
Vậy A = 1343 hay A = -1343