cho tam giác đều ABC có trọng tâm G. Tìm góc giữa GB, GC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
E
2

23 tháng 8 2021
Xét tam giác đều ABC có
G là trọng tâm của tam giác(gt)
=> 3 đường trung tuyến bằng nhau
=> \(GB=GC=AG=\dfrac{2}{3}AM=\dfrac{2}{3}.3=2\left(cm\right)\)
23 tháng 8 2021
cho tam giác abc nhọn có góc ACB=50 độ, h là trực tâm tam giác ABC. khẳng định nào dưới đây sai:
A. góc AHB=130 độ B.góc HBC=40 độ C. góc HAC=BHC D. góc A> góc B>góc C ( bạn nhớ giải thích dùm mk nha)
TT
0

PT
1

CM
21 tháng 9 2019
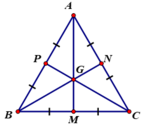
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
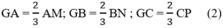
Từ (1) , (2) ⇒ GA = GB = GC.
US
1

7 tháng 4 2016
GA=GB=GC, G là trọng tâm tam giác kkhi và chỉ khi đso là tam giác đều.
Đề sai
H
0

CT
0


Gọi cạnh của tam giác là a
\(GB=GC=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý cosin cho tam giác BCG:
\(cos\widehat{BGC}=\dfrac{GB^2+GC^2-BC^2}{2GB.GC}=\dfrac{2.\left(\dfrac{a\sqrt{3}}{3}\right)^2-a^2}{2\left(\dfrac{a\sqrt{3}}{3}\right)^2}=-\dfrac{1}{2}\)
\(\Rightarrow\widehat{BGC}=120^0\)