4x2(x-2)+3x-6=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a,4x^2+(x-1)^2-(2x+1)^2=0`
`<=>4x^2+3x(-x-2)=0`
`<=>x(4x-3x-6)=0`
`<=>x(x-6)=0`
`<=>` $\left[ \begin{array}{l}x=0\\x=6\end{array} \right.$
`b)(x^2-3x)^2+5(x^2-3x)+6=0`
Đặt `x^2-3x=a(a>=-9/4)`
`pt<=>a^2+5a+6=0`
`<=>(a+2)(a+3)=0`
`<=>` $\left[ \begin{array}{l}a=-2\\a=-3(l)\end{array} \right.$
`<=>x^2-3x=-2`
`<=>x^2-3x+2=0`
`<=>(x-1)(x-2)=0`
`<=>` $\left[ \begin{array}{l}x=2\\x=1\end{array} \right.$

\(1,\Leftrightarrow x\left(x-9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=9\\x=0\end{matrix}\right.\\ 2,\Leftrightarrow x^2-4x-x^2=7\Leftrightarrow-4x=7\Leftrightarrow x=-\dfrac{7}{4}\\ 3,\Leftrightarrow3x+2x-10=5\Leftrightarrow5x=15\Leftrightarrow x=3\\ 4,\Leftrightarrow\left(5x-1\right)\left(5x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\\ 5,\Leftrightarrow\left(x-2\right)\left(3x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\\ 6,\Leftrightarrow\left(x-7\right)\left(3x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-\dfrac{4}{3}\end{matrix}\right.\)
\(7,\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\\ 8,\Leftrightarrow\left(x-4\right)\left(10x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=4\end{matrix}\right.\\ 9,\Leftrightarrow2x^2-5x-2x^2=0\Leftrightarrow x=0\\ 10,\Leftrightarrow2x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\\ 11,\Leftrightarrow\left(4x-3\right)\left(3-2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{3}{2}\end{matrix}\right.\\ 12,\Leftrightarrow2x^2-10x-2x^2=3\Leftrightarrow-10x=3\Leftrightarrow x=-\dfrac{3}{10}\)
\(1,\Leftrightarrow x\left(x-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\\ 2,\Leftrightarrow x^2-4x-x^2=7\\ \Leftrightarrow-4x=7\\ \Leftrightarrow x=\dfrac{-7}{4}\\ 3,\Leftrightarrow3x+2x-10=5\\ \Leftrightarrow5x=15\\ \Leftrightarrow x=3\\ 4,\Leftrightarrow\left(5x-1\right)\left(5x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
\(5,\Leftrightarrow\left(x-2\right)\left(3x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\\ 6,\Leftrightarrow\left(3x+4\right)\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=7\end{matrix}\right.\\ 7,\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
\(8,\Leftrightarrow10x\left(x-4\right)+2\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(10x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{1}{5}\end{matrix}\right.\\ 9,\Leftrightarrow2x^2-5x-2x^2=0\\ \Leftrightarrow-5x=0\\ \Leftrightarrow x=0\\ 10,\Leftrightarrow2x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(11,\Leftrightarrow\left(2x-3\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\\ 12,\Leftrightarrow2x^2-10x-2x^2=3\\ \Leftrightarrow-10x=3\\ \Leftrightarrow x=-\dfrac{3}{10}\)

\(a,\Leftrightarrow\left(2x-3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x^3-27-x^3+4x=1\\ \Leftrightarrow4x=28\Leftrightarrow x=7\\ c,\Leftrightarrow4x^2-4x-8=0\\ \Leftrightarrow x^2-x-2=0\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ d,\Leftrightarrow2x^2+6x+x+3=0\\ \Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)

\(a,\left(3x-7\right)^2=\left(2-2x\right)^2\)
a,\(=>\left(3x-7\right)^2-\left(2-2x\right)^2=0\)
\(< =>\left(3x-7+2-2x\right)\left(3x-7-2+2x\right)=0\)
\(< =>\left(x-5\right)\left(5x-9\right)=0=>\left[{}\begin{matrix}x=5\\x=1,8\end{matrix}\right.\)
b, \(x^2-8x+6=0< =>x^2-2.4x+16-10=0\)
\(< =>\left(x-4\right)^2-\sqrt{10}^2=0\)
\(=>\left(x-4+\sqrt{10}\right)\left(x-4-\sqrt{10}\right)=0\)
\(=>\left[{}\begin{matrix}x=4-\sqrt{10}\\x=4+\sqrt{10}\end{matrix}\right.\)
c, \(4x^2-2x-1=0\)
\(< =>\left(2x\right)^2-2.2.\dfrac{1}{2}x+\dfrac{1}{4}-\dfrac{5}{4}=0\)
\(=>\left(2x-\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{5}}{2}\right)^2=0\)
\(=>\left(2x+\dfrac{-1+\sqrt{5}}{2}\right)\left(2x-\dfrac{1+\sqrt{5}}{2}\right)=0\)
\(=>\left[{}\begin{matrix}x=\dfrac{1-\sqrt{5}}{4}\\x=\dfrac{1+\sqrt{5}}{4}\end{matrix}\right.\)
d,\(x^4-4x^2-32=0\)
đặt \(t=x^2\left(t\ge0\right)=>t^2-4t-32=0\)
\(< =>t^2-2.2t+4-6^2=0\)
\(=>\left(t-2\right)^2-6^2=0=>\left(t-8\right)\left(t+4\right)=0\)
\(=>\left[{}\begin{matrix}t=8\left(tm\right)\\t=-4\left(loai\right)\end{matrix}\right.\)\(=>x=\pm\sqrt{8}\)

\(a,\) PT thứ 2 bị lỗi rồi bạn, dấu '' = '' đou
\(b,\)
\(4x^2-32=0\Leftrightarrow4x^2=32\Leftrightarrow x^2=8\Leftrightarrow x=\pm\sqrt{8}\)
\(3x^2=48\Leftrightarrow x^2=16\Leftrightarrow x=\pm4\)
Vậy 2 pt trên không tường đương

\(a,6\left(x^2-2x+3\right)=2\left(3x^2-6x+9\right)\)
\(\Leftrightarrow6x^2-12x+18=6x^2-12x+18\)
\(\Leftrightarrow\) pt vô nghiệm
\(3x-6=3\left(x-2\right)\)
\(\Leftrightarrow3x-6=3x-6\)
\(\Leftrightarrow\) pt vô nghiệm
Vậy 2 pt tương đương
\(b,4x^2-32=0\Leftrightarrow x^2=8\Leftrightarrow x=\pm\sqrt{8}\)
\(3x^2=48\Leftrightarrow x=\pm4\)
Vậy 2 pt ko tương đương
Phương trình b tương đương vì chúng có cùng tập nghiệm là S={4;-4}
a: 6(x^2-2x+3)=2(3x^2-6x+9)
=>6x^2-12x+18=6x^2-12x+18
=>-12x=-12x
=>0x=0(luôn đúng)
3x-6=3(x-2)
=>3x-6=3x-6
=>0x=0(luôn đúng)
=>Hai phương trình tương đương

a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
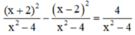
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
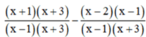
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)

a: (x^2+9)(9x^2-1)=0
=>9x^2-1=0
=>x^2=1/9
=>x=1/3 hoặc x=-1/3
b: (4x^2-9)(2^(x-1)-1)=0
=>4x^2-9=0 hoặc 2^(x-1)-1=0
=>x^2=9/4 hoặc x-1=0
=>x=1;x=3/2;x=-3/2
c: (3x+2)(9-x^2)=0
=>(3x+2)(3-x)(3+x)=0
=>\(\left[{}\begin{matrix}3x+2=0\\3-x=0\\3+x=0\end{matrix}\right.\Leftrightarrow x\in\left\{-\dfrac{2}{3};3;-3\right\}\)
d: (3x+3)^2(4x-4^2)=0
=>3x+3=0 hoặc 4x-16=0
=>x=4 hoặc x=-1
e: \(2^{\left(x-5\right)\left(x+2\right)}=1\)
=>(x-5)(x+2)=0
=>x-5=0 hoặc x+2=0
=>x=5 hoặc x=-2
4x2.(x - 2) + 3x - 6 = 0
<=> 4x2.(x - 2) + 3.(x - 2) = 0
<=> (x - 2).(4x2 + 3) = 0
<=> x - 2 = 0 hoặc 4x2 + 3 = 0
<=> x = 2 hoặc 4x2 = -3
<=> x = 2 hoặc x2 = -3/4 (vô lí) (vì \(x^2\ge0\forall x\))
<=> x = 2
Vậy: x = 2