thpt
1 trên x - 2 - 1 trên x + 2 + 4x - x2 trên 4 - x2
tick ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
25 tháng 11 2021
+ \(xy\left(3x-2y\right)-2xy^2\)
\(=xy\left(3x-2y-2y\right)\)
\(=3x^2y\)
+ \(\left(x^2+4x+4\right)\left(x+2\right)\)
\(=\left(x+2\right)^2\left(x+2\right)\)
\(=\left(x+2\right)^3\)
+ \(\dfrac{2\left(x-1\right)}{x^2}-\dfrac{x}{x-1}\)
\(=\dfrac{2\left(x-1\right)^2-x^3}{x^2\left(x-1\right)}\)
\(=\dfrac{2\left(x^2-2x+1\right)-x^3}{x^2\left(x-1\right)}\)
\(=\dfrac{2x^2-4x+2-x^3}{x^2\left(x-1\right)}\)
\(=\dfrac{-x^3+2x^2-4x+1}{x^2\left(x-1\right)}\)
21 tháng 12 2020
\(\frac{x^2+2}{2xy^3}-\frac{2x+2}{2xy^3}=\frac{x^2+2-2x-2}{2xy^3}=\frac{x^2-2x}{2xy^3}=\frac{x\left(x-2\right)}{2xy^3}=\frac{x-2}{2y^3}\)
\(\frac{4}{x-5}-\frac{1}{x+5}+\frac{13x-x^2}{25-x^2}=\frac{4}{x-5}-\frac{1}{x+5}+\frac{x^2-13x}{x^2-25}\)
\(=\frac{4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\frac{x-5}{\left(x-5\right)\left(x+5\right)}+\frac{x^2-13x}{\left(x-5\right)\left(x+5\right)}\)
\(=\frac{4x+20-x+5+x^2-13x}{\left(x-5\right)\left(x+5\right)}\)
\(=\frac{x^2-10x+25}{\left(x-5\right)\left(x+5\right)}=\frac{\left(x-5\right)^2}{\left(x-5\right)\left(x+5\right)}=\frac{x-5}{x+5}\)
1 tháng 2 2024
b:
ĐKXĐ: \(x\notin\left\{0;2;-2\right\}\)
\(\left(\dfrac{4}{x^3-4x}+\dfrac{1}{x+2}\right):\left(\dfrac{x-2}{x^2+2x}-\dfrac{x}{2x+4}\right)\)
\(=\left(\dfrac{4}{x\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}\right):\left(\dfrac{x-2}{x\left(x+2\right)}-\dfrac{x}{2\left(x+2\right)}\right)\)
\(=\dfrac{4+x\left(x-2\right)}{x\left(x-2\right)\cdot\left(x+2\right)}:\dfrac{2\left(x-2\right)-x^2}{x\left(x+2\right)\cdot2}\)
\(=\dfrac{x^2-2x+4}{x\left(x-2\right)\left(x+2\right)}\cdot\dfrac{2x\left(x+2\right)}{-\left(x^2-2x+4\right)}\)
\(=\dfrac{-2}{x-2}\)
c:ĐKXĐ: x<>0
\(\left(x-\dfrac{3}{x}\right):\left(\dfrac{x^2+2x+1}{x}-\dfrac{2x+4}{x}\right)\)
\(=\dfrac{x^2-3}{x}:\dfrac{x^2+2x+1-2x-4}{x}\)
\(=\dfrac{x^2-3}{x}\cdot\dfrac{x}{x^2-3}\)
=1
12 tháng 12 2018
a)\(\frac{3y}{4x}+\frac{5y}{4x}=\frac{3y+5y}{4x}=\frac{8y}{4x}=\frac{2y}{x}\)
b)\(\frac{x^2+1}{2x-4}-\frac{7x}{2-x}=\frac{x^2+1}{2\left(x-2\right)}-\frac{-7x}{x-2}\)
\(=\frac{x^2+1}{2\left(x-2\right)}-\frac{-7x\times2}{\left(x-2\right)\times2}=\frac{x^2+1+14x}{2\left(x-2\right)}\)
em c.ơn trước
Y
9 tháng 2 2023
\(5,\dfrac{4}{x-2}+\dfrac{x}{x+1}-\dfrac{x^2-2}{\left(x-2\right)\left(x+1\right)}=0\left(dkxd:x\ne2;-1\right)\)
\(\Rightarrow4\left(x+1\right)+x\left(x-2\right)-x^2-2=0\)
\(\Rightarrow4x+4+x^2-2x-x^2-2=0\)
\(\Rightarrow2x+2=0\)
\(\Rightarrow x=-1\left(loai\right)\)
Vậy \(S=\varnothing\)
CM
15 tháng 3 2019
Đáp án D
Hàm số luôn xác định trên 
.
Mặt khác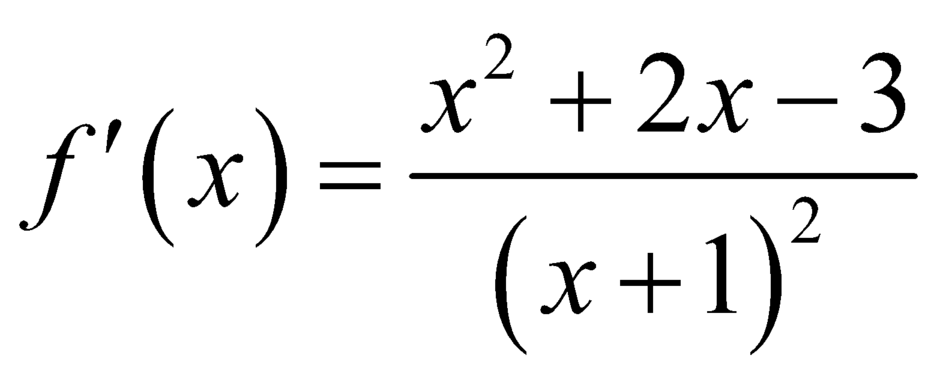 
; 
.
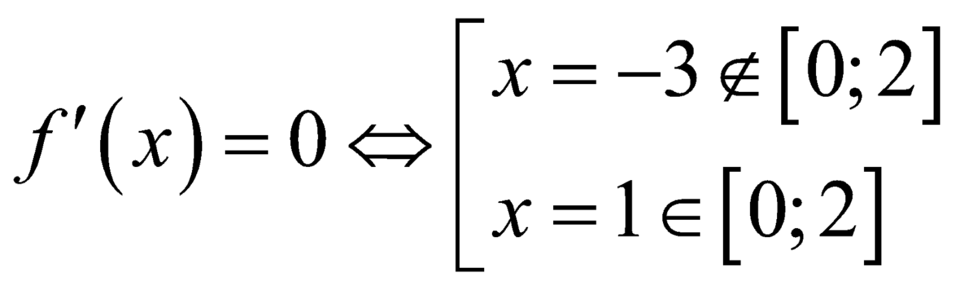Ta có: 
.
Vì vậy 
.
8 tháng 8 2023
a) Để rút gọn biểu thức (x+2)(x^2+4x+4)-(x-2)(x^2-4x-4)-12x^2-x, ta thực hiện các bước sau:
(x+2)(x^2+4x+4) = x(x^2+4x+4) + 2(x^2+4x+4)
= x^3 + 4x^2 + 4x + 2x^2 + 8x + 8
= x^3 + 6x^2 + 12x + 8
(x-2)(x^2-4x-4) = x(x^2-4x-4) - 2(x^2-4x-4)
= x^3 - 4x^2 - 4x - 2x^2 + 8x + 8
= x^3 - 6x^2 + 4x + 8
Thay vào biểu thức ban đầu, ta có:
(x+2)(x^2+4x+4)-(x-2)(x^2-4x-4)-12x^2-x
= (x^3 + 6x^2 + 12x + 8 - (x^3 - 6x^2 + 4x - 12x^2 - x
= x^3 + 6x^2 + 12x + 8 - x^3 + 6x^2 - 4x - 8 - 12x^2 - x
= 8x + 8 - 4x - 8
= 4x
Vậy biểu thức đã được rút gọn thành 4x.
b) Để rút gọn biểu thức (x-2)(x+2)(x+3)-(x+1)(x^2-x+1), ta thực hiện các bước sau:
(x-2)(x+2) = x^2 - 2^2 = x^2 - 4
Thay vào biểu thức ban đầu, ta có:
(x-2)(x+2)(x+3)-(x+1)(x^2-x+1)
= (x^2 - 4)(x+3) - (x+1)(x^2-x+1)
= x^3 + 3x^2 - 4x - 12 - (x^3 + x^2 - x + x^2 - x + 1)
= x^3 + 3x^2 - 4x - 12 - x^3 - x^2 + x - x^2 + x - 1
= x^3 - x^3 + 3x^2 - x^2 - x^2 + 3x - 4x + x - 12 - 1
= 2x^2 - x - 13
Vậy biểu thức đã được rút gọn thành 2x^2 - x - 13.
CM
16 tháng 3 2018
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)
\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x+2\right)\left(x-2\right)}+\frac{4x-x^2}{\left(2-x\right)\left(x+2\right)}\)
\(=\frac{x+2-x+2-4x+x^2}{\left(x+2\right)\left(x-2\right)}=\frac{-4x+4+x^2}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}=\frac{x-2}{x+2}\)
\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)
\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{x^2-4}\)
\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x-2\right)\left(x+2\right)}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x+2-x+2+x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x^2-4x+4}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{x-2}{x+2}\)