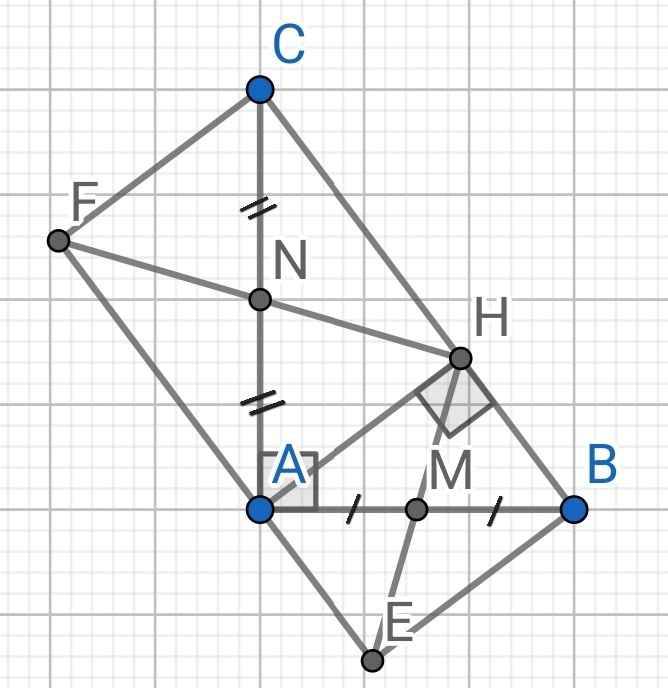
Cho ΔABC cân tại A có đường cao AH (H ∈ BC). Gọi M là TĐ của AB, E là điểm đx vs H qua M.
a) C/m: AHBE là hcn.
b) Gọi N là TĐ của AH. C/m: N là TĐ của EC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
16 tháng 10 2023
a) Do H và E đối xứng qua M (gt)
⇒ M là trung điểm HE
Tứ giác AHBE có:
M là trung điểm AB (gt)
M là trung điểm HE (cmt)
⇒ AHBE là hình bình hành
Lại có:
∠AHB = 90⁰ (AH ⊥ BC)
⇒ AHBE là hình chữ nhật
b) Do F và H đối xứng qua N
⇒ N là trung điểm của HF
Tứ giác AHCF có:
N là trung điểm AC (gt)
N là trung điểm HF (cmt)
⇒ AHCF là hình bình hành
⇒ AH = CF và AH // CF (1)
Do AHBE là hình chữ nhật (cmt)
⇒ AH // BE và AH = BE (2)
Từ (1) và (2) suy ra:
CF // BE và CF = BE
LN
13 tháng 11 2015
BẠN TỰ VẼ HÌNH NAAAAAAAA !!!!
a) Tam giác HEC có HI=IE (H đx E qua I )
EN=NC (N là trung điểm của CE )
=>IN là đường trung bình của tam giác HEC
=>IN//HC và IN=1/2HC (1)
Tam giác ACE có AI=IC , EN=NC
=>IN là đường trung bình của tam giác ACE
=>IN//AE và IN = 1/2AE (2)
Từ (1)(2) => HC//AE và HC=AE nên AHCE là hbh
Mà H=90 =>AHCE là hcn (đpcm)
b)Tam giác AHC có trung tuyến HI và t/tuyến AM cắt nhau tại G
=>G là trọng tâm của tam giác AHC
=>IG=1/3IH và IG =1/2GH
Tương tự ta có K là trọng tâm của tam giác ACE
=>IK=1/3IE và IK =1/2 KE
Mà I là trung điểm của EH =>EI=IH
=>1/3EI=1/3IH =>IG=IK
=>IG=1/2KG và EK=GH (1)
Ta có IG=1/2KG và IG =1/2 GH nên KG=GH (2)
Từ (1)(2)=>HG=GK=KE (đpcm)
D
20 tháng 7 2021
Bài 1
a/ AB // DI
Mà AM thuộc tia AB => AM // DI (1)
=> Tứ giác AIDM là hình thang
E là trung điểm của AD (gt) => ED = EA
Xét △EDI và △EAM có:
- Góc DEI = Góc AEM (đối đỉnh)
- ED = EA (cmt)
- Góc EDI = Góc EAM (slt)
=> △EDI = △EAM (g.c.g)
=> AM = DI (2)
Từ (1) và (2). Vậy: Tứ giác AIDM là hình bình hành (đpcm)
b/ Chứng minh tương tự câu a
c/ Hình bình hành BICN có: BN = IC = CD/2 (I là trung điểm của CD)
Hình bình hành AIDM có: MA = ID = CD/2 (I là trung điểm của CD)
=> BN = MA (3)
Mặt khác ta có: H là trung điểm của AB (gt) hay HA = HB (4)
Từ (3) và (4) suy ra: BN + HA = HB + MA
Hay: HM = HN
Hay: H là trung điểm của MN (đpcm
Bài 2: Đề sai nên không thể giải
24 tháng 11 2021
Xét △ABH có M là trung điểm AB
N là trung điểm AH
⇔MN là đường trung bình của △ABH
⇒MN // BH và MN=\(\dfrac{1}{2}\) BH hay MN // BC và MN=\(\dfrac{1}{4}\)BC
mà BC ⊥ AH (gt)
⇒MN ⊥ AH
e)
theo d MN=\(\dfrac{1}{4}\)BC mà BC=12
⇒MN=3
S△AMH=\(\dfrac{8.3}{2}\)=12cm2
8 tháng 11 2021
a: Xét ΔAHC có
I là trung điểm của HC
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAHC
Suy ra: IN//MH và IN=MH
hay INMH là hình bình hành
mà \(\widehat{IHM}=90^0\)
nên INMH là hình chữ nhật
16 tháng 12 2023
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ta có: ADHE là hình chữ nhật
=>AH cắt DE tại trung điểm của mỗi đường
mà O là trung điểm của AH
nên O là trung điểm của DE
c: Ta có: ADHE là hình chữ nhật
=>DH=AE và DH//AE
Ta có: DH//AE
M\(\in\)AE
Do đó: DH//AM
Ta có: DH=AE
AE=AM
DO đó: DH=AM
Xét tứ giác AHDM có
DH//AM
DH=AM
Do đó: AHDM là hình bình hành
=>AH//MD
=>AO//MD