Question

[kim ngân lê thị]

một vật trượt từ mặt phẳng nghiêng cao 10\(\sqrt{2}\) m, góc nghiêng α=45 và g=10m/s2. hệ số ma sát là 0,1.

a) tính gia tốc của  vật

b) vân tốc của vật tại mặt phẳng nghiêng

c) thời gian vật chuyển đông xuống mặt phẳng nghiêng

d) vân tốc của vật tại đồ cao 2\(\sqrt{2}\)m

Answer 1

[Hoàng Tử Hà]

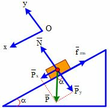
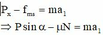
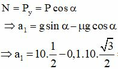
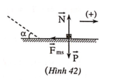
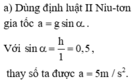
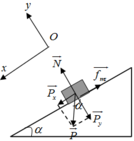
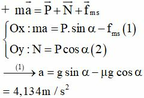
Phân tích lực theo 2 phương Ox: song song với mp nghiêng, chiều dương hướng xuống

Oy: vuông góc với mp nghiêng, chiều dương hướng lên

\(l=h.\sin\alpha=10\sqrt{2}.\dfrac{\sqrt{2}}{2}=10\left(m\right)\)

\(\left\{{}\begin{matrix}Ox:P\cos\alpha-F_{ms}=ma\\Oy:P\sin\alpha=N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mg\cos\alpha-\mu N=m.a\\N=P\sin\alpha\end{matrix}\right.\Leftrightarrow g\cos\alpha-\mu g\sin\alpha=a=...\left(m/s^2\right)\)

b/ \(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{2.a.l}=...\left(m/s\right)\)

c/ \(t=\dfrac{v-v_0}{a}=\dfrac{v}{a}=...\left(s\right)\)

d/ \(l'=h'\sin\alpha=2\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\left(m\right)\)

\(v'^2=2aS\Rightarrow v=\sqrt{2.a.l'}=...\left(m/s\right)\)