cho nửa đường tròn tâm 0 đường kính AB cố định .trên cùng 1 nửa mặt phẳng bờ AB chứa đg tròn vẽ tiếp tuyến Ax,By trên nửa đg tròn ấy lấy điểm C bất kỳ vẽ tiếp tuyến tại C cắt Ax,By tại D và E . cm AD+BE=DE AC cắt DO tại M ,BC cắt OE tại N tứ giác CMON ? .cm OM×OD+ON×OE ko đổi . AN cắt CO tại H điểm H di chuyển trên đg nào khi C di chuyển trên nửa đg tròn tâm O
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

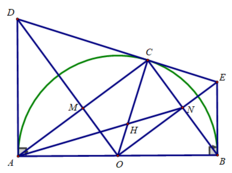
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE

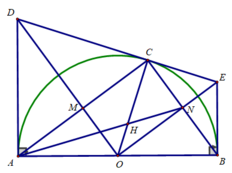
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi

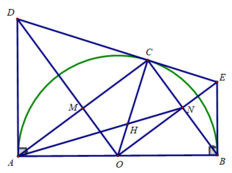
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
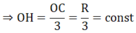
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)

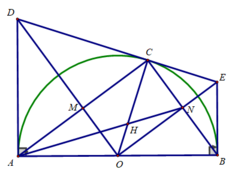
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

a: Xét (O) có
DA là tiếp tuyến có A là tiếp điểm
DC là tiếp tuyến có C là tiếp điểm
Do đó: DA=DC
Xét (O) có
EC là tiếp tuyến có E là tiếp điểm
EB là tiếp tuyến có B là tiếp điểm
Do đó: EC=EB
Ta có: CD+CE=DE
nên DA+EB=DE

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔADB vuông tại A có AC là đường cao
nên \(AD^2=DB\cdot DC\)
b: Xét (O) có
EC là tiếp tuyến
EA là tiếp tuyến
Do đó: EC=EA
=>ΔECA cân tại C
=>góc ECA=góc EAC
\(\Leftrightarrow90^0-\widehat{ECA}=90^0-\widehat{EAC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
=>ΔECD cân tại E
=>ED=EC
mà EC=EA
nên EA=ED
hay E là trung điểm của AD

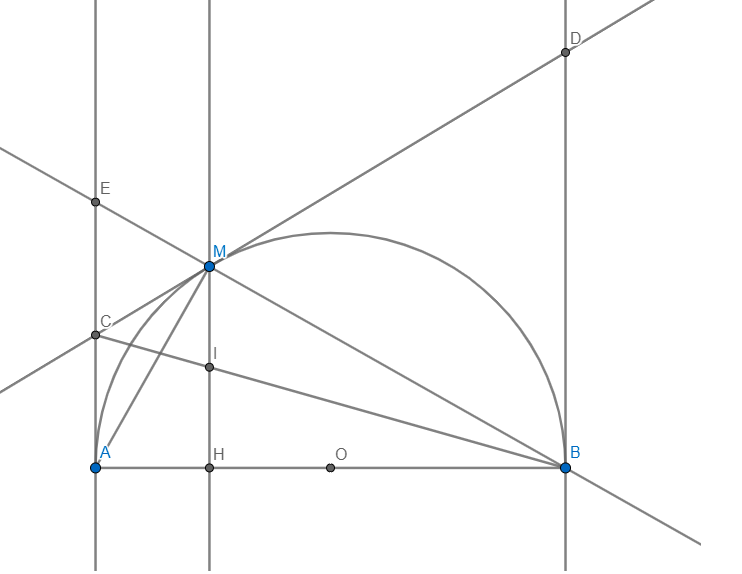
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm
a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi