Cho ΔABC .Tìm điểm M thõa mãn \(\overrightarrow{MA}+\overrightarrow{AB}=\overrightarrow{CB}+\overrightarrow{AC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|\overrightarrow{MA}+\overrightarrow{BC}+\overrightarrow{AB}\right|=\left|\overrightarrow{AC}+\overrightarrow{BA}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MA}+\overrightarrow{AC}\right|=\left|\overrightarrow{BC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MC}\right|=\left|\overrightarrow{BC}\right|\)
\(\Leftrightarrow MC=BC\)
\(\Rightarrow\) Tập hợp M là đường tròn tâm C bán kính BC

\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow MG=\dfrac{1}{3}BC\)
Tập hợp M là đường tròn tâm G bán kính \(R=\dfrac{BC}{3}\)

Dựng hình bình hành ABDC \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{BA}+\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|\overrightarrow{AD}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MD}\right|=\left|\overrightarrow{MA}\right|\)
\(\Leftrightarrow MD=MA\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng AD

Qua A dựng đường thẳng d song song BC, trên d lấy điểm I sao cho \(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{BC}\)
\(\Rightarrow3\overrightarrow{IA}=2\overrightarrow{BC}\Rightarrow3\overrightarrow{IA}+2\overrightarrow{CB}=\overrightarrow{0}\)
Ta có:
\(\left|3\overrightarrow{MA}+2\overrightarrow{MB}-2\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MA}+2\left(\overrightarrow{MB}+\overrightarrow{CM}\right)\right|=\left|\overrightarrow{MB}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MA}+2\overrightarrow{CB}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MI}+3\overrightarrow{IA}+2\overrightarrow{CB}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MI}\right|=\left|\overrightarrow{CB}\right|\)
\(\Leftrightarrow MI=\dfrac{1}{3}BC\)
Tập hợp M là đường tròn tâm I bán kính \(\dfrac{BC}{3}\)

Do G là trọng tâm ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Do I là trung điểm BC \(\Rightarrow\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}\)
\(2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=3.\left|2\overrightarrow{MI}\right|\)
\(\Leftrightarrow2.\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=6\left|\overrightarrow{MI}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MG}\right|=6\left|\overrightarrow{MI}\right|\)
\(\Leftrightarrow MG=MI\)
Tập hợp M là đường trung trực của đoạn thẳng IG

a. Xem lại đề bài, trị tuyệt đối đầu tiên 2 biểu thức MC trừ đi nhau thấy ko đúng
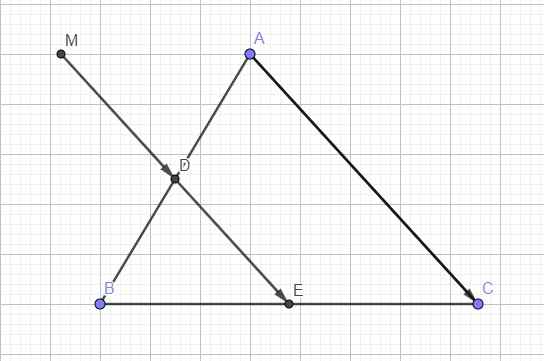
b. Gọi D là trung điểm AB, E là trung điểm BC
\(\Rightarrow\) DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{AC}\) \(\Rightarrow\overrightarrow{AC}=2\overrightarrow{DE}\)
Ta có:
\(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{AC}\Leftrightarrow2\overrightarrow{MD}=2\overrightarrow{DE}\) (do D là trung điểm AB nên \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MD}\))
\(\Rightarrow\overrightarrow{MD}=\overrightarrow{DE}\Rightarrow D\) là trung điểm ME
\(\Rightarrow\) M là điểm đối xứng E qua D

Gọi P và Q lần lượt là trung điểm AB và CD \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MP}\\\overrightarrow{MC}+\overrightarrow{MD}=2\overrightarrow{MQ}\end{matrix}\right.\)
\(\left|\overrightarrow{MA}-\overrightarrow{BM}\right|=\left|\overrightarrow{MC}-\overrightarrow{DM}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MC}+\overrightarrow{MD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MP}\right|=\left|2\overrightarrow{MQ}\right|\)
\(\Leftrightarrow MP=MQ\)
Tập hợp M là đường trung trực của đoạn PQ

Gọi G là trọng tâm tam giác ABC
\(\vec{MA}.\vec{MB}+\vec{MB}.\vec{MC}+\vec{MC}.\vec{MA}\)
\(=\dfrac{1}{2}\left(\vec{MA}+\vec{MB}+\vec{MC}\right)^2-\dfrac{1}{2}\left(MA^2+MB^2+MC^2\right)\)
\(\ge-\dfrac{1}{2}\left(MA^2+MB^2+MC^2\right)\)
\(=-\dfrac{1}{2}\left[\left(\vec{MG}+\vec{GA}\right)^2+\left(\vec{MG}+\vec{GB}\right)^2+\left(\vec{MG}+\vec{GC}\right)^2\right]\)
\(=-\dfrac{1}{2}\left[3MG^2+2\vec{MG}\left(\vec{GA}+\vec{GB}+\vec{GC}\right)+GA^2+GB^2+GC^2\right]\)
\(\ge-\dfrac{1}{2}\left(GA^2+GB^2+GC^2\right)\)
\(min=-\dfrac{1}{2}\left(GA^2+GB^2+GC^2\right)\Leftrightarrow M\equiv G\)
Lời giải:
\(\overrightarrow{MA}=\overrightarrow{CB}+\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{AB}-\overrightarrow{AB}=\overrightarrow{0}\)
$\Rightarrow M\equiv A$